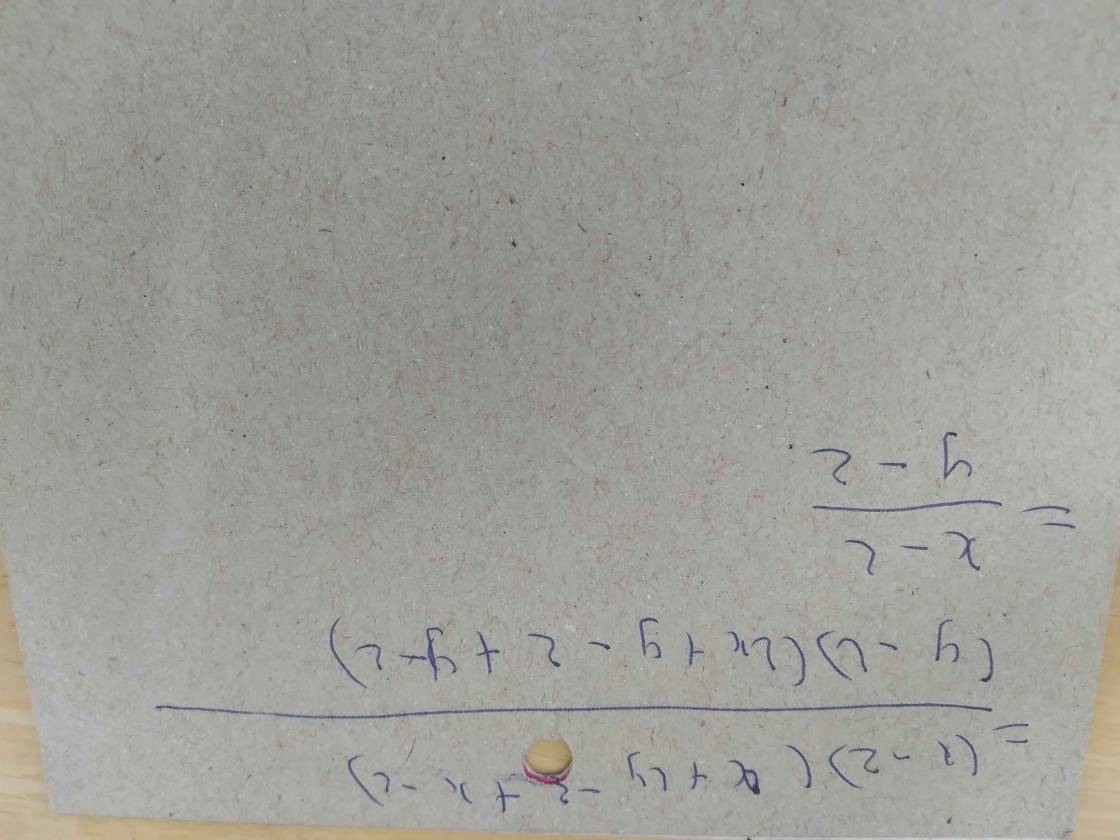cho x2 = y ; y2 = xz ; x + y +z ≠ 0 và x,z,y là các số khác 0. Tính ( x+y+z)999/ x222.y333.z444

Những câu hỏi liên quan
Cho đồ thị của các hàm số sau:
(1): y = - 2 x 2
(2): y = x 2
(3): y = -3 x 2
(4): y = -10 x 2
Hỏi có bao nhiêu đồ thị hàm số nằm phía dưới trục hoành?
A. 1
B. 2
C. 3
D. 4
Đáp án C
Đồ thị hàm số y = a x 2 (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục tung làm đối xứng.
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành.
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành.
Trong đồ thị các hàm số đã cho; các đồ thị nằm phía dưới trục hoành là”
(1): y = -2 x 2 ; (3): y = - 3 x 2 và (4):y = -10 x 2
Đúng 0
Bình luận (0)
Cho biết x là tỉ lệ thuận với y theo hệ số tỉ lệ a. Cho bản giá trị sau x -4 x2 y y1 -2 A. y1-1, x2-2B. y12 , x21C. y11 , x28D. y1-1 , x22(giải thích) Cảm ơn!!
Đọc tiếp
Cho biết x là tỉ lệ thuận với y theo hệ số tỉ lệ a. Cho bản giá trị sau
| x | -4 | x2 |
| y | y1 | -2 |
A. y1=-1, x2=-2
B. y1=2 , x2=1
C. y1=1 , x2=8
D. y1=-1 , x2=2
(giải thích)
Cảm ơn!!
1 .cho x + y = 2 và x2 + y2 = 16 . Tính x3 + y3
2. cho x + y = 8 và xy = -20 . Tính x2 + y2 ; x3 + y3 ; và x2 + xy + y2
giúp ạ , cảm cơn
1)
Ta có: x+y=2
nên \(\left(x+y\right)^2=4\)
\(\Leftrightarrow x^2+y^2+2xy=4\)
\(\Leftrightarrow2xy=2\)
hay xy=1
Ta có: \(x^3+y^3\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(=2^3-3\cdot1\cdot2\)
=2
2)\(x^2+y^2=\left(x+y\right)^2-2xy=8^2-2\cdot\left(-20\right)=104\)
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=8^3-3\cdot\left(-20\right)\cdot8=512+480=992\)
\(x^2+y^2+xy=\left(x+y\right)^2-xy=8^2-\left(-20\right)=64+20=84\)
Đúng 1
Bình luận (0)
Cho x2+y2=(x+y-z)2
CMR x2+(x-z)2/y2+(y-z)2 =x-z/y-z
cho x,y∈ R ; x≠y
tìm min P=x2-6xy+6y2/x2-2xy+y2
\(P=\dfrac{x^2-6xy+6y^2}{x^2-2xy+y^2}=\dfrac{-3\left(x^2-2xy+y^2\right)+4x^2-12xy+9y^2}{x^2-2xy+y^2}\)
\(=-3+\left(\dfrac{2x-3y}{x-y}\right)^2\ge-3\)
\(P_{min}=-3\) khi \(2x=3y\)
Đúng 3
Bình luận (0)
Cho x2+y2+z2=2 tìm GTLN P=x2/x2+yz+x+1 + y+z/x+y+z+1 + 1/xyz+3
bài 1: cho các số dương x, y, z thỏa mãn x+y+z=1. Tìm min
a) A = x2+y2+z2
b) B = x2+y2+3z2
c) C=x2+2y2+3z2
d) D=x2+by2+cz2
Cho đồ thị hàm số y = x 2 và y = 3 x 2 . Tìm giao điểm của hai đồ thị hàm số đã cho?
A. O(0; 0)
B. A(1; 1)
C. O(0; 0) và A(1; 1)
D. O(0; 0) và B( 1; 3)
Đáp án A
Hoành độ giao điểm của hai đồ thị hàm số đã cho là nghiệm phương trình:
x2 = 3x2 ⇔ -2x2 = 0 ⇔ x = 0
Với x = 0 thì y= 02 = 0
Do đó,đồ thị hai hàm số đã cho cắt nhau tại điểm duy nhất là gốc tọa độ O(0; 0).
Đúng 0
Bình luận (0)
Cho các phản ứng sau: X
→
X1 + CO2 ; X1 + H2O
→
X2; X2 + Y
→
X + Y1 + H2O ; X2 + 2Y
→
X+Y2 + 2H2O. X, Y lần lượt là: A. BaCO3 và Na2CO3 B. MgCO3 và NaHCO3 C. CaCO3 và NaHCO3 D. CaCO3 và NaHSO4
Đọc tiếp
Cho các phản ứng sau: X → X1 + CO2 ; X1 + H2O → X2; X2 + Y → X + Y1 + H2O ;
X2 + 2Y → X+Y2 + 2H2O. X, Y lần lượt là:
A. BaCO3 và Na2CO3
B. MgCO3 và NaHCO3
C. CaCO3 và NaHCO3
D. CaCO3 và NaHSO4
Đáp án C
CaCO3(X) → CaO(X1) + CO2
CaO(X1) + H2O → Ca(OH)2(X2)
Ca(OH)2(X2) + NaHCO3(Y) → CaCO3(X) + NaOH(Y1) + H2O
Ca(OH)2(X2) + 2NaHCO3(Y) → CaCO3(X) + Na2CO3(Y2) +2H2O
Đúng 0
Bình luận (0)
Cho x-y+1=0. Tính giá trị của biểu thức
M= x2(x-y) + y2(y-x)+x2-y2+100
M=x^2*(-1)-y^2(x-y)+x^2-y^2+100
=-x^2+y^2+x^2-y^2+100
=100
Đúng 0
Bình luận (0)