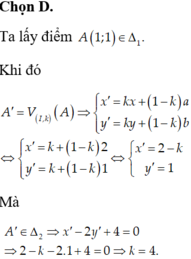Trong một mặt phẳng với hệ trục tọa độ oxy cho 2 đường thẳng d1: x+2y-5=0; d2 3x+my-1=0. Điều kiện của tham số m để góc tạo bởi hai đương thẳng bằng 45 độ.

Những câu hỏi liên quan
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
3
-
1
y
-
3
-
2
z
+
2
1
và
d...
Đọc tiếp
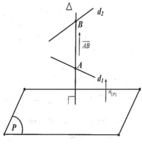
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 và d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P) có phương trình x+2y+3z-5=0. Đường thẳng Δ vuông góc với (P) cắt d1 và d2 có phương trình là:
![]()
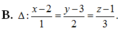
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
3
-
1
y
-
3
-
2
z
+
2
1
và...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 và d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P) có phương trình x + 2 y + 3 z - 5 = 0 . Đường thẳng Δ vuông góc với (P) cắt d 1 và d 2 có phương trình là:
A. ∆ : x - 1 1 = y + 1 2 = z 3
B. ∆ : x - 2 1 = y - 3 2 = z - 1 3
C. ∆ : x - 3 1 = y - 3 2 = z + 2 3
C. ∆ : x - 1 3 = y + 1 2 = z 1
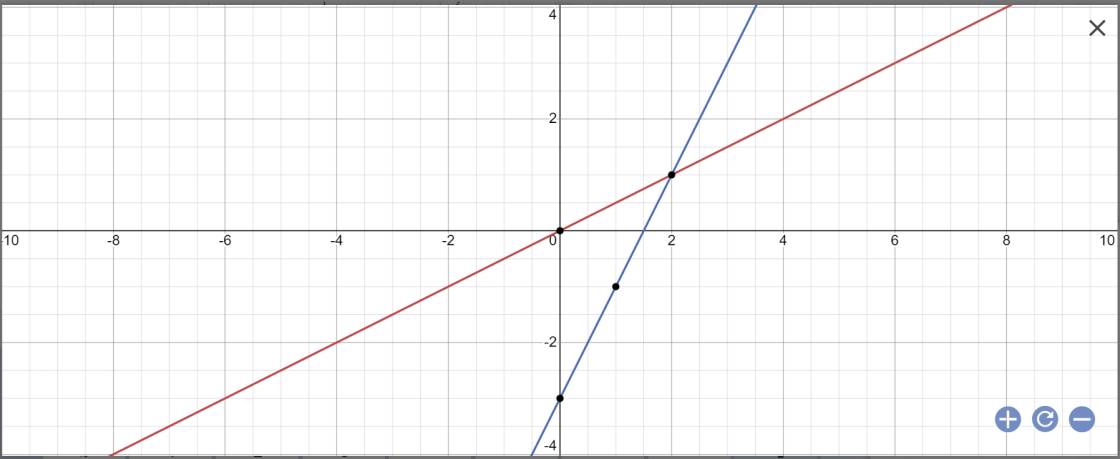
Trong mặt phẳng tọa độ Oxy Cho hàm số y = 2 x - 3 có đồ thị là đường thẳng d1 và hàm số y = 1/2 x có đồ thị là đường thẳng d2 a vẽ đồ thị d1 và d2 trên cùng hệ trục tọa độ
Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng
d
1
:
2
x
+
3
y
+
1
0
và
d
2
:
x
-
y
-
2
0
Có bao nhiêu phép tịnh tiến biến...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng d 1 : 2 x + 3 y + 1 = 0
và d 2 : x - y - 2 = 0 Có bao nhiêu phép tịnh tiến biến d 1 thành d 2
A.Vô số
B.4
C.1
D.0
Chọn D.
Vì d 1 không song song hoặc trùng với d 2 nên không tồn tại phép tịnh tiến nào biến d 1 thành d 2
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, tính góc tạo giữa 2 đường thẳng
d1 : x + \(\sqrt{3}\) y =0 và d2 : x+10=0
(d1): x+căn 3y=0
=>VTPT là \(\left(1;\sqrt{3}\right)\)
(d2): x+10=0
=>x+0y+10=0
=>VTPT là (1;0)
\(cos\left(d1;d2\right)=\left|\dfrac{1\cdot1+\sqrt{3}\cdot0}{\sqrt{1^2+3}\cdot\sqrt{1^2}}\right|=\left|\dfrac{1}{2}\right|=\dfrac{1}{2}\)
=>(d1;d2)=60 độ
Đúng 2
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng
d
1
:
y
2
x
−
3
y
+
1
0
và
d
2
:
x
+
y
−
2
0.
Có bao nhiêu phép tịnh tiến biến
d
1
thành
d...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d 1 : y = 2 x − 3 y + 1 = 0 và d 2 : x + y − 2 = 0. Có bao nhiêu phép tịnh tiến biến d 1 thành d 2
A. Vô số
B. 0
C. 1
D. 4
trong mặt phẳng tọa độ oxy cho các đường thẳng (d1): -2x+5y-8=0;(d2): x+2y-5=0;(d3): (m^2-1)x+3y-5-2m=0.xác định m để ba đường thẳng trên là ba đường thẳng phân biệt đồng quy
Tọa độ giao điểm của đường thẳng (d1) và (d2) là:
\(\left\{{}\begin{matrix}-2x+5y-8=0\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Để 3 đường thẳng trên đồng qua thì:
\(\left(m^2-1\right)x+3y-5-2m=0\\ \Leftrightarrow\left(m^2-1\right).1+3.2-5-2m=0\\ \Leftrightarrow m^2-1+6-5-2m=0\\ \Leftrightarrow m^2-2m=0\\ \Leftrightarrow m\left(m-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}-2x+5y-8=x+2y-5\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x+y=1\\x+2y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
Thay x=1 và y=2 vào (d3), ta được:
\(m^2-1+3\cdot2-5-2m=0\)
\(\Leftrightarrow m\left(m-2\right)=0\)
hay \(m\in\left\{0;2\right\}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ trục tọa độ Oxy Cho hai đường thẳng
∆
1
và
∆
2
lần lượt có phương trình: x-2x+10 và x-2y+40,điểm I(2;1) Phép vị tự tâm I tỉ số k biến đường thẳng
∆
1
thành
∆
2
. Tìm k ? A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ
Oxy Cho hai đường thẳng ∆ 1 và ∆ 2
lần lượt có phương trình: x-2x+1=0
và x-2y+4=0,điểm I(2;1) Phép vị tự
tâm I tỉ số k biến đường thẳng ∆ 1
thành ∆ 2 . Tìm k ?
A. 1
B. 2
C. 3
D. 4
Trong mặt phẳng hệ trục tọa độ Oxy cho 2 đường thẳng (d1):y=x+3-2m và (d2):y=-3x+4m-2.Tìm m để (d1)&(d2) cắt nhau tại một điểm thuộc vào đường phân giác thứ nhất