Xét các số thực a; b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của P của biểu thức P = log a b 2 a 2 + 3 log b a b
A. 19.
B. 13.
C. 14.
D. 15.
Xét phương trình a x 3 − x 2 + b x − 1 = 0 với a, b là các số thực, a ≠ 0 , a ≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 − 3 a b + 2 a 2 b − a .
A. 15 3 .
B. 8 2 .
C. 11 6 .
D. 12 3 .
Xét các số thực dương a,b thỏa mãn: log9a = log12b = log15(a+b). Tính \(\dfrac{a}{b}\)
Đặt \(log_9a=log_{12}b=log_{15}\left(a+b\right)=t\Rightarrow\left\{{}\begin{matrix}a=9^t\\b=12^t\\a+b=15^t\end{matrix}\right.\)
\(\Rightarrow9^t+12^t=15^t\)
\(\Rightarrow\left(\dfrac{3}{5}\right)^t+\left(\dfrac{4}{5}\right)^t=1\)
Hàm \(f\left(t\right)=\left(\dfrac{3}{5}\right)^t+\left(\dfrac{4}{5}\right)^t\) có \(f'\left(t\right)=\left(\dfrac{3}{5}\right)^tln\left(\dfrac{3}{5}\right)+\left(\dfrac{4}{5}\right)^t.ln\left(\dfrac{4}{5}\right)< 0\Rightarrow\) nghịch biến trên R
\(\Rightarrow f\left(t\right)\) có tối đa 1 nghiệm \(\Rightarrow t=2\) là nghiệm duy nhất
\(\Rightarrow\dfrac{a}{b}=\left(\dfrac{3}{4}\right)^2=\dfrac{9}{16}\)
Xét phương trình ax3- x2+ bx-1=0 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 - 3 a b + 2 a 2 ( b - a ) .
A. 15 3
B. 8 2
C. 11 6
D. 12 3
Giả sử phương trình đã cho có 3 nghiệm
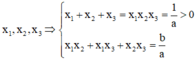
Khi đó
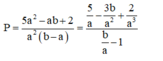
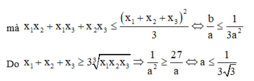
Suy ra
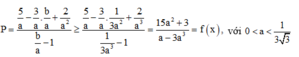
Xét hàm số:
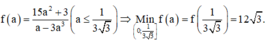
Chọn D.
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
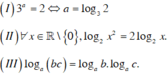
Trong ba mệnh đề (I),(II),(III), số mệnh đề sai là
A. 2
B. 0
C. 3
D. 1
xét các số thực dương a,b thỏa mãn a+b=2 . tìm Max của biểu thức P=a2b
xét các số thực dương a,b thỏa mãn a+b=2. Tìm max của biểu thức P=a^2*b
Lời giải:
Áp dụng BĐT Cô-si:
\(2=a+b=\frac{a}{2}+\frac{a}{2}+b\geq 3\sqrt[3]{\frac{a^2b}{4}}\)
\(\Rightarrow \frac{2}{3}\geq \sqrt[3]{\frac{a^2b}{4}}\Rightarrow \frac{8}{27}\geq \frac{a^2b}{4}\)
\(\Leftrightarrow a^2b\leq \frac{32}{27}\Leftrightarrow P\leq \frac{32}{27}\)
Vậy $P_{\max}=\frac{32}{27}$. Giá trị này đạt tại $\frac{a}{2}=b=\frac{2}{3}$
Xét hàm số f liên tục trên R và các số thực a, b, c tùy ý. Trong các khẳng định sau, khẳng định nào sai?
A. ∫ a b f x d x = ∫ c b f x d x - ∫ c a f x d x
B. ∫ a b f x d x = ∫ a c f x d x + ∫ c b f x d x
C. ∫ a b f x d x = ∫ a c f x d x - ∫ c b f x d x
D. ∫ a b f x d x = ∫ a c f x d x - ∫ b c f x d x
Xét các số thực a,b thỏa b > 1 , a ≤ b < a . Biểu thức P = log a b b a + 2 log b a đạt giá trị khỏ nhất khi
A. a = b 2
B. a 2 = b 3
C. a 3 = b 2
D. a 2 = b
Dễ dàng biến đổi được ![]()
Từ điều kiện, suy ra a > 1
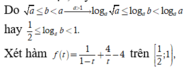 ta được f(t) đạt giá trị nhỏ nhất bằng 5 khi
ta được f(t) đạt giá trị nhỏ nhất bằng 5 khi ![]()
Chọn B.
Xét các số thực a, b thỏa mãn a > b > 1. Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b .
A. P min = 19.
B. P min = 13.
C. P min = 14.
D. P min = 15.
Xét các số thực a, b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b
A. P m i n = 19
B. P m i n = 13
C. P m i n = 14
D. P m i n = 15