Cho ABCD là hình chữ nhật (AB>AD). Điểm E thuộc AD ; I,K thuộc CD sao cho DI=CK. Đường thẳng vuông góc vời EK tại K cắt BC tại M.
Tính góc EIM
Những câu hỏi liên quan
cho hình chữ nhật ABCD có E ,F lần lượt là trung điểm của AB,CD.Gọi O là giao điểm của AB và BD
a) CM : DEBF là hình bình hành
b) CM: 3 điểm E ; O ; F thẳng hàng
c ) Biết AD/AB = 2/3 và hình chữ nhật ABCD có diện tích 96 cm vuông . Tính AD ; AB?
a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
Đúng 0
Bình luận (0)
cho hình chữ nhật ABCD và điểm E thuộc đường chéo BD . qua E kẻ đường thẳng song song với AC cắt AD , AB tại M và N vẽ hình chữ nhật. a] chứng minh AF // BD b] chứng minh E là trung điểm CF
Xem chi tiết
a] Để chứng minh AF // BD, ta cần chứng minh tỉ số đồng dạng giữa các cặp cạnh tương ứng của hai tam giác ACF và BDE. Ta có:
AC/BD = AD/BE (vì AF // BD) AC/AD = BE/BD (vì AM // BD và BN // BD)
Từ hai tỉ số trên, ta có:
AC/AD = BE/BD
Vậy, ta đã chứng minh được AF // BD.
b] Để chứng minh E là trung điểm CF, ta cần chứng minh CE = EF và CF // AB. Ta có:
CE = AM (vì CE // AM và AC // BD) EF = BN (vì EF // BN và AC // BD)
Vậy, ta đã chứng minh được E là trung điểm CF.
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD. Điểm E thuộc cạnh AD, điểm F thuộc cạnh AB. Gọi I, K, M, N theo thứ tự là trung điểm của EF, FD, BE, BD. Chứng minh IN = KM
HS chứng minh IMNK là hình chữ nhật Þ IN = KM
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD E thuộc AD ,F thuộc AB gọi I,K,M,N theo thứ tự là trung điểm của EF ,FD, BE, BD.Chứng minh IN=KM
Gấp một mảnh giấy hình chữ nhật ABCD như hình vẽ sao cho điểm D trùng với điểm E (E thuộc BC) Tính CE, biết AD=10cm,AB=8 cm
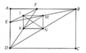
Cho hình vuông ABCD cạnh y (cm). Điểm E thuộc cạnh AB. Điểm G thuộc tia AD sao cho AG = AD + (3/2)EB. Dựng hình chữ nhật GAEF. Đặt EB = 2x (cm).
Tính x và y để diện tích hình chữ nhật bằng diện tích hình vuông và ngũ giác ABCFG có chu vi bằng 100 + 4 13 (cm).
Vì E thuộc cạnh AB nên EB < AB hay 2x < y
Ta có: AE = AB – EB = y – 2x (cm)
AG = AD + DG = y + (3/2) EB = y + (3/2) .2x = y + 3x (cm)
Diện tích hình chữ nhật bằng diện tích hình vuông nên ta có phương trình:
(y – 2x)(y + 3x) = y 2
Theo định lí Pitago, ta có: F C 2 = E B 2 + D G 2
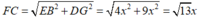
Chu vi ngũ giác ABCFG:
PABCFG = AB + BC + CF + FG + GA
= AB + BC + CF + FG + GD + DA
= y + y + x 13 + y – 2x + 3x + y = x(1 + 13 ) + 4y
Vì chu vi ngũ giác ABCFG bằng 100 + 4 13 (cm) nên ta có phương trình:
x(1 + 13 ) + 4y = 100 + 4 13
Ta có hệ phương trình:
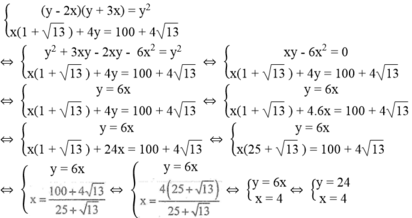
Giá trị của x và y thỏa điều kiện bài toán.
Vậy x = 4 (cm), y = 24 (cm).
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD. Gọi I là trung điểm AB, M thuộc cạnh AD sao cho AD=3AM, N thuộc đoạn ID sao cho ND=2IN. Chứng minh \(N\in AC\)
Cho hình chữ nhật ABCD có Ab=30 cm ;AD=20cm.Lấy các điểm E,F,J,Htheo thứ tự thuộc cạnh Ab,BC,CD,Da sao cho Ae=Ah=CF=CG=x.Tính x để EFGH là hình thoi
Cho hình chữ nhật ABCD có O là giao điểm của AC và BD. Lấy một điểm E bất kì trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EFEC. Vẽ FH và FK lần lượt vuông góc với AB và AD (H thuộc AB, K thuộc AD).a) Chứng minh: BD2AO.(đã làm)b) Gọi I là giao điểm của KH và AF. Chứng minh I là trung điểm của KH.c) Chứng minh tứ giác AIEO là hình bình hành.d) Chứng minh I, K, E thẳng hàng.
Đọc tiếp
Cho hình chữ nhật ABCD có O là giao điểm của AC và BD. Lấy một điểm E bất kì trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF=EC. Vẽ FH và FK lần lượt vuông góc với AB và AD (H thuộc AB, K thuộc AD).
a) Chứng minh: BD=2AO.(đã làm)
b) Gọi I là giao điểm của KH và AF. Chứng minh I là trung điểm của KH.
c) Chứng minh tứ giác AIEO là hình bình hành.
d) Chứng minh I, K, E thẳng hàng.
a) Để chứng minh BD = 2AO, ta có thể sử dụng định lý Thales và các quy tắc về tỉ lệ đồng dạng. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
b) Để chứng minh I là trung điểm của KH, ta có thể sử dụng các quy tắc về đường thẳng song song và đồng quy. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
c) Để chứng minh tứ giác AIEO là hình bình hành, ta có thể sử dụng các quy tắc về đường chéo và cạnh đối. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
d) Để chứng minh I, K, E thẳng hàng, ta có thể sử dụng các quy tắc về đường thẳng và góc vuông. Tuy nhiên, để trình bày cách chứng minh chi tiết, tôi cần thêm thông tin về các định lý và quy tắc được sử dụng trong bài toán này.
Đúng 0
Bình luận (0)