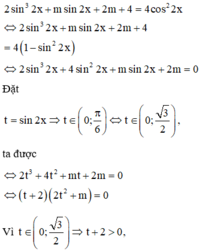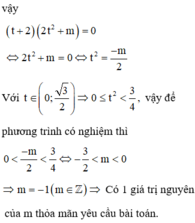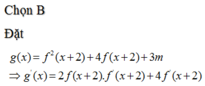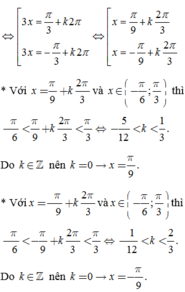Tìm tất cả các giá trị nguyên của tham số m thuộc [ -3 ; 5] để hàm số \(y=\left(2m-3\right)x+5m-1\) nghịch biến trên R

Những câu hỏi liên quan
Tìm số tất cả các giá trị nguyên của tham số thực m để phương trình
2
sin
3
2
x
+
m
sin
2
x
+
2
m
+
4
4
cos
2
2...
Đọc tiếp
Tìm số tất cả các giá trị nguyên của tham số thực m để phương trình 2 sin 3 2 x + m sin 2 x + 2 m + 4 = 4 cos 2 2 x có nghiệm thuộc 0 ; π 6
A. 4
B. 3
C. 1
D. 6
Đáp án C
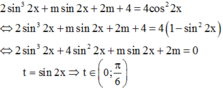
Đặt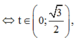
ta được
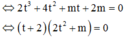
Vì 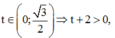
vậy
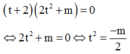
Với
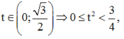
vậy để phương trình có nghiệm thì ![]()
![]()
Có 1 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Tìm số tất cả các giá trị nguyên của tham số thực m để phương trình
2
sin
3
2
x
+
m
sin
2
x
+
2
m
+
4
4
c
o
s
2
2
x
có nghiệm thuộc
0
;
π
6
A. 4 B. 3...
Đọc tiếp
Tìm số tất cả các giá trị nguyên của tham số thực m để phương trình 2 sin 3 2 x + m sin 2 x + 2 m + 4 = 4 c o s 2 2 x có nghiệm thuộc 0 ; π 6
A. 4
B. 3
C. 1
D. 6
a) Tìm tất cả các giá trị của tham số m để gleft(xright)4mx^2-4left(m-1right)x+m-3 luôn luôn âm với mọi x thuộc Rb) Tìm tất cả các giá trị của tham số m để fleft(xright)x^2-2left(m+2right)x-2m^2+3m+4 không âm với mọi m thuộc Rc) Bất pt x^2+2mx+m^2-5m+60 ( m là tham số thực) có nghiệm với mọi x thuộc R khi minleft(-infty;dfrac{a}{b}right) với a,bin Z và dfrac{a}{b} là phân số tối giản. Tính giá trị biểu thức a+2b
Đọc tiếp
a) Tìm tất cả các giá trị của tham số m để \(g\left(x\right)=4mx^2-4\left(m-1\right)x+m-3\) luôn luôn âm với mọi x thuộc R
b) Tìm tất cả các giá trị của tham số m để \(f\left(x\right)=x^2-2\left(m+2\right)x-2m^2+3m+4\) không âm với mọi m thuộc R
c) Bất pt \(x^2+2mx+m^2-5m+6>0\) ( m là tham số thực) có nghiệm với mọi x thuộc R khi \(m\in\left(-\infty;\dfrac{a}{b}\right)\) với \(a,b\in Z\) và \(\dfrac{a}{b}\) là phân số tối giản. Tính giá trị biểu thức a+2b
tìm tất cả các giá trị nguyên của tham số m để bất phương trình x^2 -2.(m-1).x+4.m+8>=0 nghiệm đúng với mọi x thuộc R
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=\left(m-1\right)^2-\left(4m+8\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow m^2-6m-7\le0\)
\(\Rightarrow-1\le m\le7\)
\(\Rightarrow m=\left\{-1;0;1;2;3;4;5;6;7\right\}\)
Đúng 1
Bình luận (0)
Cho hàm số
y
f
x
có đồ thị như hình bên dưới Gọi S là tập hợp tất cả các giá trị nguyên của tham số
m
∈
-
100
;
100
để hàm số
h
x
f
2
x
+
2...
Đọc tiếp
Cho hàm số y = f x có đồ thị như hình bên dưới
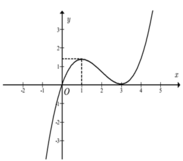
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m ∈ - 100 ; 100 để hàm số h x = f 2 x + 2 + 4 f x + 2 + 3 m có đúng 3 điểm cực trị. Tổng giá trị của tất cả các phần tử thuộc S bằng
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để phương trình
4
log
4
2
x
−
2
log
2
x
+
3
−
m
0
có nghiệm thuộc đoạn
2
;
4
.
A.
2
≤
m
≤
3
. B.
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 4 log 4 2 x − 2 log 2 x + 3 − m = 0 có nghiệm thuộc đoạn 2 ; 4 .
A. 2 ≤ m ≤ 3 .
B. 2 ≤ m ≤ 4 .
C. 3 ≤ m ≤ 4 .
D. 1 ≤ m ≤ 2 .
Đáp án A
Điều kiện: x > 0 .
4 log 4 2 x − 2 log 2 x + 3 − m = 0 ⇔ 4. 1 4 . log 2 2 x − 2 log 2 x + 3 − m = 0 ⇔ log 2 2 x − 2 log 2 x + 3 − m = 0 1 .
Đặt t = log 2 x ta có (1) tương đương
t 2 − 2 t + 3 − m = 0 ⇔ t 2 − 2 t + 3 = m .
Ta tìm giá trị của m để t 2 − 2 t + 3 − m = 0 có nghiệm thuộc đoạn 1 ; 2 .
Khảo sát hàm y t = t 2 − 2 t + 3.
Ta có y ' t = 2 t − 2 = 0 ⇔ t = 1.
Bảng biến thiên
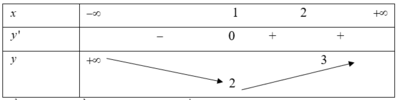
Để thỏa mãn đề bài thì 2 ≤ m ≤ 3 .
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
4
log
2
4
x
−
2
log
2
x
+
3
−
m
0
có nghiệm thuộc đoạn
1
2
;
4
.
A.
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 4 log 2 4 x − 2 log 2 x + 3 − m = 0 có nghiệm thuộc đoạn 1 2 ; 4 .
A. 2 ; 3
B. 11 4 ; 15
C. 11 4 ; 9
D. 2 ; 6
Đáp án D
Điều kiện: x > 0.
Đặt t = log 2 x . Khi đó
4 log 2 4 x − 2 log 2 x + 3 − m = 0 ⇔ 4. 1 4 log 2 2 x − 2 log 2 x + 3 − m = 0 ⇔ t 2 − 2 t + 3 − m = 0.
Để thỏa mãn đề bài thì phương trình t 2 − 2 t + 3 − m = 0 có nghiệm thuộc đoạn − 1 ; 2
t 2 − 2 t + 3 − m = 0 ⇔ t 2 − 2 t + 3 = m .
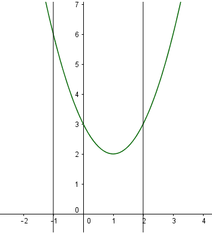
Từ đồ thị hàm số y = t 2 − 2 t + 3 nhân thấy 2 ≤ m ≤ 6 thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)
Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình
6
x
−
3
−
m
2
x
−
m
0
có nghiệm thuộc khoảng (0;1) A.
2
;
4
. B.
3
;
4...
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình 6 x − 3 − m 2 x − m = 0 có nghiệm thuộc khoảng (0;1)
A. 2 ; 4 .
B. 3 ; 4 .
C. 2 ; 4 .
D. 3 ; 4 .
Đáp án C
6 x − 3 − m 2 x − m = 0 ⇔ m = 6 x + 3.2 x 2 x + 1
Xét hàm số f x = 6 x + 3.2 x 2 x + 1 trên khoảng 0 ; 1
f ' x = 6 x .2 x ln 6 − ln 2 + 6 x ln 6 + 3.2 x ln 2 2 x + 1 2 > 0 do đó hàm số y = f x đồng biến trên khoảng 0 ; 1 .
Phương trình f x = m có nghiệm trong khoảng 0 ; 1 ⇔ f 0 < m < f 1 ⇔ 2 < m < 4 .
Đúng 0
Bình luận (0)
Cho hàm số f(x) = \(\dfrac{x^3}{3}-mx^2+\left(m+2\right)x+3\). Có tất cả các giá trị nguyên của tham số m để f'(x) ≥ 0 với mọi thuộc R.
Tìm tất cả các giá trị thực của tham số m để phương trình
2
cos
2
3
x
+
3
−
2
m
cos
3
x
+
m
−
2
0
có đúng 3 nghiệm thuộc khoảng
−
π
6
;
π...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 cos 2 3 x + 3 − 2 m cos 3 x + m − 2 = 0 có đúng 3 nghiệm thuộc khoảng − π 6 ; π 3
A. − 1 ≤ m ≤ 1
B. 1 < m ≤ 2
C. 1 ≤ m ≤ 2
D. 1 ≤ m < 2