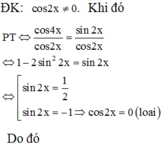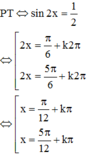107. Pt √3 . tan2x +3=0 có bao nhiêu nghiệm thuộc khoảng (2000π ; 2018π) ( căn ngang số 3 thôi nhé)
A. 37
B. 40
C. 36
D. 35
108. Pt cos5x = 1/√2 có bao nhiêu nghiệm thuộc đoạn [-50π ; 0]
A. 124
B. 125
C. 250
D. 249
109. Pt sin2x = -1/2 có bao nhiêu nghiệm thuộc khoảng (0;π)
A. 1
B. 3
C. 2
D. 4
110. Pt 1+ 2cos2x =0 có nghiệm là? ( Bấm máy)