Đặt \(f\left( x \right) = \sqrt {x - 1}  + \sqrt {2 - x} \)

Với mọi \({x_0} \in \left( {1;2} \right)\), ta có:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {\sqrt {x - 1}  + \sqrt {2 - x} } \right) = \mathop {\lim }\limits_{x \to {x_0}} \sqrt {x - 1}  + \mathop {\lim }\limits_{x \to {x_0}} \sqrt {2 - x} \\ & \,\,\,\,\, = \sqrt {\mathop {\lim }\limits_{x \to {x_0}} x - \mathop {\lim }\limits_{x \to {x_0}} 1}  + \sqrt {\mathop {\lim }\limits_{x \to {x_0}} 2 - \mathop {\lim }\limits_{x \to {x_0}} x}  = \sqrt {{x_0} - 1}  + \sqrt {2 - {x_0}}  = f\left( {{x_0}} \right)\end{array}\)

Vậy hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( {1;2} \right)\).

Ta có:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {\sqrt {x - 1}  + \sqrt {2 - x} } \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {\sqrt {x - 1}  + \sqrt {2 - x} } \right)\\ &  = \sqrt {\mathop {\lim }\limits_{x \to {1^ + }} x - \mathop {\lim }\limits_{x \to {1^ + }} 1}  + \sqrt {\mathop {\lim }\limits_{x \to {1^ + }} 2 - \mathop {\lim }\limits_{x \to {1^ + }} x}  = \sqrt {1 - 1}  + \sqrt {2 - 1}  = 1 = f\left( 1 \right)\end{array}\)

\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\sqrt {x - 1}  + \sqrt {2 - x} } \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\sqrt {x - 1}  + \sqrt {2 - x} } \right)\\ &  = \sqrt {\mathop {\lim }\limits_{x \to {2^ - }} x - \mathop {\lim }\limits_{x \to {2^ - }} 1}  + \sqrt {\mathop {\lim }\limits_{x \to {2^ - }} 2 - \mathop {\lim }\limits_{x \to {2^ - }} x}  = \sqrt {2 - 1}  + \sqrt {2 - 2}  = 1 = f\left( 2 \right)\end{array}\)

Vậy hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {1;2} \right]\).

a) \(f\left( 3 \right) = 1 - {3^2} = 1 - 9 =  - 8\).

\(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \left( {1 - {x^2}} \right) = 1 - {3^2} = 1 - 9 =  - 8\).

Vì \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right) =  - 8\) nên hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0} = 3\).

b) \(f\left( 1 \right) =  - 1\).

\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^2} + 1} \right) = {1^2} + 1 = 2\).

\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( { - x} \right) =  - 1\).

Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\)

Vậy hàm số không liên tục tại điểm \({x_0} = 1\).

ĐKXĐ: \({x^2} - 4 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 2\\x \le  - 2\end{array} \right.\)

Vậy hàm số có TXĐ: \(D = \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)\).

Hàm số \(y = \sqrt {{x^2} - 4} \) là hàm số căn thức nên nó liên tục trên các nửa khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {2; + \infty } \right)\).

Ta có: \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \sqrt {{x^2} - 4}  = \sqrt {{2^2} - 4}  = 0 = f\left( 2 \right)\)

\(\mathop {\lim }\limits_{x \to  - {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to  - {2^ + }} \sqrt {{x^2} - 4}  = \sqrt {{{\left( { - 2} \right)}^2} - 4}  = 0 = f\left( { - 2} \right)\)

Vậy hàm số \(y = \sqrt {{x^2} - 4} \) liên tục trên các nửa khoảng \(\left( { - \infty ; - 2} \right]\) và \(\left[ {2; + \infty } \right)\).

1.

\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{2x}{x\left(\sqrt{x+2}+\sqrt{2-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{2}{\sqrt{x+2}+\sqrt{2-x}}=\dfrac{2}{2\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)

Vậy cần bổ sung \(f\left(0\right)=\dfrac{\sqrt{2}}{2}\) để hàm liên tục tại \(x=0\)

2.

a. \(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x+\dfrac{3}{2}\right)=\dfrac{3}{2}\)

\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}{x\left(\sqrt[]{x+1}+1\right)}\)

\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1}{\sqrt[]{x+1}+1}=\dfrac{3}{2}\)

\(\Rightarrow f\left(0\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\) nên hàm liên tục tại \(x=0\)

2b.

\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\dfrac{x^3-x^2+2x-2}{x-1}=\lim\limits_{x\rightarrow1^-}\dfrac{x^2\left(x-1\right)+2\left(x-1\right)}{x-1}\)

\(=\lim\limits_{x\rightarrow1^-}\dfrac{\left(x^2+2\right)\left(x-1\right)}{x-1}=\lim\limits_{x\rightarrow1^-}\left(x^2+2\right)=3\)

\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)=\lim\limits_{x\rightarrow1^+}\left(3x+a\right)=a+3\)

- Nếu \(a=0\Rightarrow f\left(1\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^+}f\left(x\right)\) hàm liên tục tại \(x=1\)

- Nếu \(a\ne0\Rightarrow\lim\limits_{x\rightarrow1^-}f\left(x\right)\ne\lim\limits_{x\rightarrow1^+}f\left(x\right)\Rightarrow\) hàm không liên tục tại \(x=1\)

a. ĐKXĐ: \(-3\le x\le3\)

\(y'=1-\dfrac{x}{\sqrt{9-x^2}}=\dfrac{\sqrt{9-x^2}-x}{\sqrt{9-x^2}}=0\Rightarrow x=\dfrac{3\sqrt{2}}{2}\)

Dấu của y':

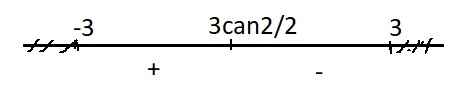
Hàm đồng biến trên \(\left(-3;\dfrac{3\sqrt{2}}{2}\right)\) và nghịch biến trên \(\left(\dfrac{3\sqrt{2}}{2};3\right)\)

b.

ĐKXĐ: \(x\ne2\)

\(y'=\dfrac{\left(-2x-1\right)\left(x+2\right)+x^2+x+2}{\left(x+2\right)^2}=\dfrac{-x^2-4x}{\left(x+2\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)

Dấu của y':

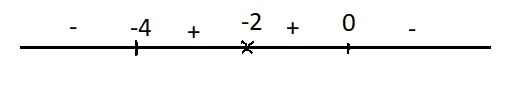
Hàm đồng biến trên các khoảng \(\left(-4;-2\right)\) và \(\left(-2;0\right)\)

Hàm nghịch biến trên các khoảng \(\left(-\infty;-4\right)\) và \(\left(0;+\infty\right)\)

a) Dễ thấy x = 0 thuộc tập xác định của hàm số.

\(f\left( 0 \right) = {0^2} + 1 = 1\)

Ta có:       \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {{x^2} + 1} \right) = {0^2} + 1 = 1\)

                   \(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {1 - x} \right) = 1 - 0 = 1\)

Vì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = 1\) nên \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = 1 = f\left( 0 \right)\).

Vậy hàm số liên tục tại điểm \(x = 0\).

b)Dễ thấy x = 1 thuộc tập xác định của hàm số.

\(f\left( 1 \right) = {1^2} + 2 = 3\)

Ta có:       \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^2} + 2} \right) = {1^2} + 2 = 3\)

                   \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} x = 1\)

Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).

Vậy hàm số không liên tục tại điểm \(x = 1\).

a)     Ta có:

\(\left. \begin{array}{l}f\left( { - x} \right) = \sin \left( { - x} \right).\cos \left( { - x} \right) =  - \sin x.\cos x\\f\left( x \right) = \sin x.\cos x\end{array} \right\} \Rightarrow f\left( { - x} \right) =  - f\left( x \right)\)

Hàm số \(y = \sin x\cos x\) là hàm số lẻ

b)     Ta có:

\(\left. \begin{array}{l}f\left( { - x} \right) = \tan \left( { - x} \right) + \cot \left( { - x} \right) =  - \tan x - \cot x\\f\left( x \right) = \tan x + \cot x\end{array} \right\} \Rightarrow f\left( { - x} \right) =  - f\left( x \right)\)

Hàm số \(y = \tan x + \cot x\) là hàm số lẻ

c)     Ta có:

 \(\left. \begin{array}{l}f\left( { - x} \right) = {\sin ^2}\left( { - x} \right) = {\left( { - \sin \left( x \right)} \right)^2} = {\sin ^2}x\\f\left( x \right) = {\sin ^2}x\end{array} \right\} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)

Hàm số \(y = {\sin ^2}x\) là hàm số chẵn

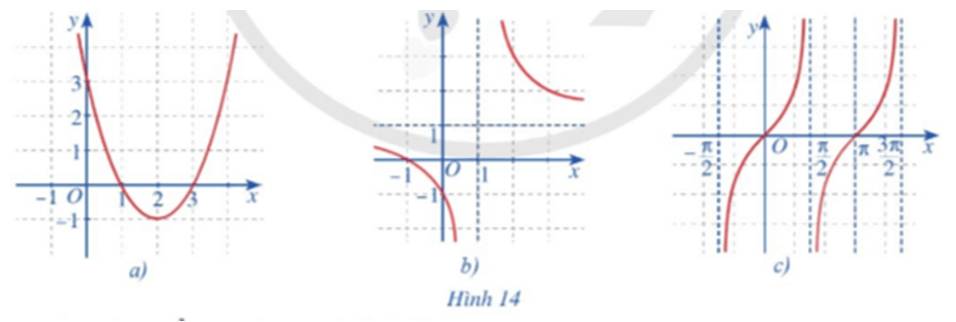
Hình 14a đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ trên khoảng xác định.

Hình 14b đồ thị bị chia làm hai nhánh:

- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.

- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.

Vậy hàm số liên tục trên từng khoảng xác định.

Hình 14c đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.