cho △DEF có \(\widehat{D}\)=60\(^0\); \(\widehat{E}\)=60\(^0\). trên tia đối của tia DE lấy điểm G. vẽ góc EGy so le trong với góc DEF và EGy=60\(^0\). vẽ Dx là tia phân giác của GDE. chứng minh:
a)Gy // Dx
b)Dx // EF
Những câu hỏi liên quan
Cho \(\Delta DEF\)có \(\widehat{D}=60^0,\widehat{E}=60^{0.}\). Trên tia đối của tia DE lấy điểm G. Vẽ góc EGH so le trong với góc E và \(\widehat{EGH}=60^0\) Vẽ Dx là tia phân giác của GDF. Chứng minh:
a, GH // Dx
b, Dx // EF
a) Hình tự vẽ dễ dàng.
Ta có : \(\widehat{E}=\widehat{EGH}=60^o\)mà hai góc này nằm ở vị trí so le trong => GH//Dx ( điều phải chứng minh ).
b) Ta có : \(\widehat{GDF}\&\widehat{D}\)là hai góc nằm ở vị trí kề bù
\(\Rightarrow\widehat{GDF}+\widehat{D}=180^o\Leftrightarrow\widehat{GDF}=180^o-\widehat{D}=180^o-60^o=120^o\)
Vì Dx là tia phân giác góc GDF nên : \(\widehat{GDx}=\widehat{FDx}=\frac{\widehat{GDF}}{2}=\frac{120^o}{2}=60^o\)( 1 )
Áp dụng tính chất tổng ba góc trong 1 tam giác : \(\widehat{E}+\widehat{D}+\widehat{F}=180^o\Leftrightarrow\widehat{F}=180^o-\widehat{E}-\widehat{D}=180^o-60^o-60^o=60^o\)( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\widehat{FDx}=\widehat{F}=60^o\)mà hai góc này nằm ở vị trí so le trong => Dx//EF ( điều phải chứng minh ).
Đúng 0
Bình luận (0)
Cho ΔABC ∽ ΔDEF. Biết \(\widehat A = {60^o};\widehat E = {80^o}\), hãy tính số đo các góc \(\widehat B,\widehat C,\widehat D,\widehat E\)
Vì ΔABC ∽ ΔDEF \( \Rightarrow \widehat A = \widehat D{,^{}}\widehat B = \widehat E{,^{}}\widehat C = \widehat F\)
Mà \(\widehat A = {60^o} \Rightarrow \widehat D = {60^o}\)
\(\widehat E = {80^o} \Rightarrow \widehat B = {80^o}\)
Có \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat C = \widehat F = {180^o} - {60^o} - {80^o} = {40^o}\)
Đúng 0
Bình luận (0)
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE\), \(\widehat {ABC} = \widehat {DEF} = {70^\circ },\widehat {BAC} = \widehat {EDF} = {60^\circ },AC = 6\;{\rm{cm}}.\)
Tính độ dài cạnh DF.
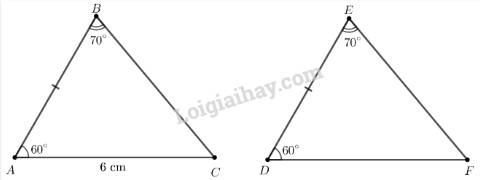
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}\widehat {ABC} = \widehat {DEF} (= {70^\circ })\\AB = DE\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\( \Rightarrow \Delta ABC{\rm{ = }}\Delta DEF\)(g.c.g)
\( \Rightarrow DF = AC\)( 2 cạnh tương ứng)
Mà AC = 6 cm
\( \Rightarrow DF = 6cm\)
Đúng 0
Bình luận (0)
Cho \(\Delta ABC = \Delta DEF\). Biết rằng \(\widehat A = {60^\circ },\hat E = {80^\circ }\), tính số đo các góc B, C, D, F.
Do \(\Delta ABC = \Delta DEF\) nên \(\widehat B = \widehat E = {80^o}\); \(\widehat D = \widehat A = {60^o}\); \(\widehat C = \widehat F\) ( các góc tương ứng)
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 60^\circ + 80^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ - 60^\circ - 80^\circ = 40^\circ \end{array}\)
Do đó \(\widehat F = 40^\circ \)
Vậy \(\widehat B = {80^o}; \widehat D ={60^o}; \widehat C = \widehat F= 40^\circ \).
Đúng 0
Bình luận (0)
Các tam giác vuông ABC và DEF có \(\widehat{A}=\widehat{D}=90^0;AC=DF;\widehat{B}=\widehat{E}\). Các tam giác vuông đó có bằng nhau không ?
Xét hai tam giác vuông ABC và DEF có:
AC = DF (gt)
\(\widehat{ABC}=\widehat{DEF}\) (gt)
Vậy: \(\Delta ABC=\Delta DEF\left(cgv-gn\right)\).
Đúng 0
Bình luận (0)
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE,AC = DF,\widehat {BAC} = \widehat {EDF} = {60^\circ },BC = 6\;{\rm{cm}},\widehat {ABC} = {45^\circ }\). Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.
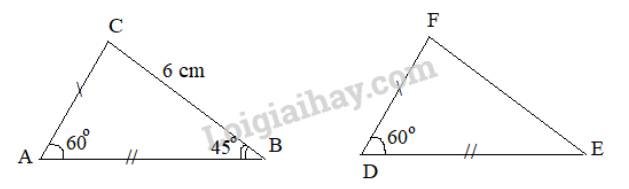
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)
Do đó:
\(BC=EF = 6cm\) ( 2 cạnh tương ứng)
\( \widehat {ABC} =\widehat {DEF}= {45^o}\) (2 góc tương ứng)
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)
\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn có góc A= 600. các đường phân giác của \(\widehat{B}\)và \(\widehat{C}\)cắt nhau tại O và cắt AC, AB lần lượt tại E, D. tia phân giác của \(\widehat{BOC}\)cắt BC tại F
a) tính \(\widehat{BOC}\)
b) chứng minh BD+CE=BC
c) chứng minh tam giác DEF đều
Các tam giác vuông ABC và DEF có \(\widehat{A}=\widehat{D}=90^0\). AC = DF. Hãy bổ sung thêm một điều kiện bằng nhau (về cạnh hay về góc) để \(\Delta ABC=\Delta DEF\) ?
Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm ˆCC^=ˆFF^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)
Đúng 0
Bình luận (0)
Giải:
Xem hình vẽ
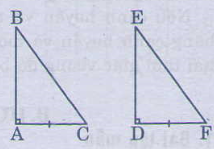
* Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm ˆCC^=ˆFF^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)
Đúng 0
Bình luận (2)
Các tam giác vuông ABC và DEF có A^=D^=900. AC = DF. Hãy bổ sung thêm một điều kiện bằng nhau (về cạnh hay về góc) đểΔABC=ΔDEF?
Giải:
Xem hình vẽ
* Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm C^=F^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)
ΔABC=ΔDEF?
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC, có \(\widehat{ASB\:=}90^0,\widehat{BSC}=60^0,\widehat{CSA}=120^0.\) Tính khoảng cách từ C đến (SAB).
A. \(\dfrac{a}{4}\)
B. a
C. \(\dfrac{a}{2}\)
D. \(\dfrac{3a}{2}\)
