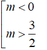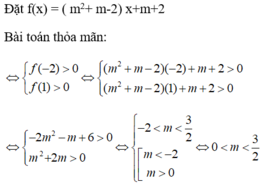1) Tìm m để mọi x\(\in[0;+\infty)\) đều là nghiệm của bất phương trình: (m2-1)x2-8mx+9-m2\(\ge\)0
2) Cho hàm số f(x)= x2+bx+1 với b∈(3;\(\frac{7}{2}\)\()\). giải bất phương trình f(f(x))>x
3) Tìm m để bất phương trình 2x2-(2m+1)x+m2-2m+2≤0 nghiệm đúng với mọi x ∈ \(\left[\frac{1}{2};2\right]\)