Cho hình vẽ trên , biết
\(\widehat{AMC}=\widehat{BMA}+\widehat{MCD};\) :
\(\widehat{BAN}+\widehat{ANE}+\widehat{NEF}=360^0\)
CMR : CD // EF
Bài 1: Cho hình vẽ, biết \(n\perp AB\) tại B, \(\widehat{F_1}\)=\(120^o\).
a) Chứng tỏ m//n.
b) Tính \(\widehat{E_1}\).
c) Chứng tỏ \(m\perp AB\). Vì sao?
Trên mặt phẳng, cho đoạn thẳng BC=2a(a>0), lấy 1 điểm A bất kì sao cho tam giác ABC nhọn. Các đường cao AD,BR,CF cắt nhau tại H (D,E,F lần lượt nắm trên các cạnh BC, CA, AB). Trên các đoạn HB, HC lần lượt lấy M, N sao cho \(\widehat{AMC}=\widehat{BNA}=90^o\)
a) chứng minh tam giác AMN cân
b) tìm GTLN của BN.CM theo a
Tính chất cơ bản của tam giác với 3 đường cao: \(\Delta AEF\sim\Delta ABC\) (bài toán quen thuộc chắc em tự c/m được)
\(\Rightarrow AF.AB=AE.AC\)
Trong tam giác vuông ABN với đường cao NF:
\(AN^2=AF.AB\)
Trong tam giác vuông ACM:
\(AM^2=AE.AC\)
\(\Rightarrow AM^2=AN^2\Rightarrow AM=AN\)
b. Hệ thức lượng: \(BN^2=BF.AB\) ; \(CM^2=CE.AC\)
\(\Delta ABD\sim\Delta CBF\) (2 tam giác vuông chung góc B)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BD}{BF}\Rightarrow BF.AB=BD.BC\) (1)
Hoàn toàn tương tư, \(\Delta ADC\sim\Delta BEC\Rightarrow CE.AC=CD.BC\) (2)
Cộng vế (1) và (2) \(\Rightarrow BF.AB+CE.AC=\left(BD+CD\right)BC=BC^2\)
\(\Rightarrow BN^2+CM^2=BC^2\)
\(\Rightarrow BN.CM\le\dfrac{1}{2}\left(BN^2+CM^2\right)=\dfrac{1}{2}BC^2=2a^2\)
Dấu "=" xảy ra khi tam giác cân tại A
a) Trong Hình 20a, cho biết \(\widehat N = \widehat E,\widehat M = \widehat D,MP = 18m,DF = 24m,\)\(EF = 32m,\)\(NP = a + 3\left( m \right)\). Tìm \(a\).
b) Cho \(ABCD\) là hình thang \(\left( {AB//CD} \right)\) (Hình 20b).
Chứng minh rằng \(\Delta AMB\backsim\Delta CMD\). Tìm \(x,y\).

a) Xét tam giác \(MNP\) tam giác \(DEF\) ta có:
\(\widehat M = \widehat D\) (giả thuyết)
\(\widehat N = \widehat E\) (giả thuyết)
Do đó, \(\Delta MNP\backsim\Delta DEF\) (g.g)
Suy ra, \(\frac{{MP}}{{DF}} = \frac{{NP}}{{EF}} \Rightarrow \frac{{18}}{{24}} = \frac{{a + 2}}{{32}} \Rightarrow a + 2 = \frac{{18.32}}{{24}} = 24 \Leftrightarrow a = 24 - 2 = 22\).
Vậy \(a = 22m\).
b) Vì \(ABCD\) là hình thang nên \(AB//CD\).
Vì \(AB//CD \Rightarrow \widehat {ABM} = \widehat {MDC}\) (hai góc so le trong) và \(AB//CD \Rightarrow \widehat {BAM} = \widehat {MCD}\) (hai góc so le trong)
Xét tam giác \(AMB\) và tam giác \(CMD\) có:
\(\widehat {ABM} = \widehat {MDC}\) (chứng minh trên)
\(\widehat {BAM} = \widehat {MCD}\) (chứng minh trên)
Do đó, \(\Delta AMB\backsim\Delta CMD\) (g.g).
Ta có:
\(\frac{{AM}}{{CM}} = \frac{{BM}}{{DM}} = \frac{{AB}}{{CD}} \Leftrightarrow \frac{6}{{15}} = \frac{y}{{10}} = \frac{8}{x}\).
Ta có: \(\frac{6}{{15}} = \frac{y}{{10}} \Rightarrow y = \frac{{10.6}}{{15}} = 4\)
\(\frac{6}{{15}} = \frac{8}{x} \Rightarrow x = \frac{{8.15}}{6} = 20\).
Vậy \(x = 20;y = 4\).
Cho \(\Delta\)ABC có AB<AC , M là trung điểm BC . Trên tia đối của MA lấy điểm D sao cho MA=MA . C/M rằng :
a) \(\widehat{BMA}=\widehat{CDM}\)
b) \(\widehat{BMA>}\widehat{MAC}\)
HELP ME !!!
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: BA//DC
=>\(\widehat{BAM}=\widehat{CDM}\)
b: Ta có: \(\widehat{BAM}=\widehat{CDM}\)
mà \(\widehat{CDM}>\widehat{MAC}\)(DA>DC)
nên \(\widehat{BAM}>\widehat{MAC}\)
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Điều nào dưới đây không suy ra ΔABC ∽ ΔDEF
A. \(\widehat B = \widehat E\)
B. \(\widehat C = \widehat F\)
C. \(\widehat B + \widehat C = \widehat E + \widehat F\)
D. \(\widehat B - \widehat C = \widehat E - \widehat F\)
Đáp án đúng là đáp án C.
Vì \(\widehat B + \widehat C = \widehat E + \widehat F\) chưa thể suy ra được \( \widehat B = \widehat E\) và \( \widehat C = \widehat F \)
Quan sát Hình 6. Vẽ vào tờ giấy tam giác \(DEF\) với \(EF = 4cm,\widehat E = 36^\circ ,\widehat F = 76^\circ \).
a) Chứng minh \(\Delta DEF\backsim\Delta AMC\).
b) Dùng thước đo chiều dài cạnh \(DF\) của \(\Delta DEF\). Tính khoảng cách giữa hia điểm \(A\) và \(C\) ở hai bờ sông trong Hình 6.

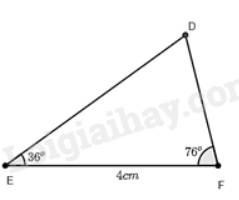
a) Xét tam giác \(DEF\) và tam giác \(AMC\) có:
\(\widehat E = \widehat M = 36^\circ \)
\(\widehat F = \widehat C = 76^\circ \) (chứng minh trên)
Suy ra, \(\Delta DEF\backsim\Delta AMC\) (g.g).
b) Đổi 25m = 2500 cm.
Dùng thước đo độ dài cạnh \(DF\) ta được độ dài \(DF\) là 2,6cm.
Vì \(\Delta DEF\backsim\Delta AMC\) nên \(\frac{{DF}}{{EF}} = \frac{{AC}}{{MC}}\) (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{2,6}}{4} = \frac{{AC}}{{2500}} \Rightarrow AC = \frac{{2,6.2500}}{4} = 1625\).
Vậy khoảng cách giữa hai điểm \(A\) và \(C\) là 1625 cm hay 16,25m.
Trong Hình 17, cho biết \(DE = 6cm,EF = 7,8cm,NP = 13cm,NM = 10cm,\widehat E = \widehat N\) và \(\widehat P = 42^\circ \). Tính \(\widehat F\).
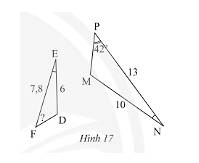
Ta có:
\(\frac{{EF}}{{NP}} = \frac{{7,8}}{{13}} = \frac{3}{5};\frac{{DE}}{{MN}} = \frac{6}{{10}} = \frac{3}{5}\)
Xét tam giác \(DEF\) và tam giác \(MNP\) ta có:
\(\frac{{EF}}{{NP}} = \frac{{DE}}{{MN}} = \frac{3}{5}\)
\(\widehat E = \widehat N\) (giải thuyết)
Do đó, \(\Delta DEF\backsim\Delta MNP\) (c.g.c)
Do đó, \(\widehat F = \widehat P = 42^\circ \).
Tam giác DEF có: DE = DF. H là trung điểm của EF, \(\widehat{E}\) bằng 50o.
a/ Tính \(\widehat{F}\)
b/ Chứng minh DH vuông góc với EF.
c/ Trên DE lấy điểm M, trên DF lấy điểm N sao cho DM - DN, và HM = HN. Chứng minh \(\widehat{DMH}=\widehat{DNH}\)
* Lưu ý: Khỏi cần vẽ hình
a,ta có;\(\widehat{E}=\widehat{F}\)(do \(DE=DF\)nên\(\Delta DEF\)cân tại D)mà\(\widehat{E}=50^0=>\widehat{F}=50^0\)
b.xét\(\Delta DEF\)cân tại D có(1)
DH là đường trung tuyến ứng với cạnh EF(do H là trung điểm của EF)(2)
từ (1) và(2)=>DH đồng thời là đường cao ứng với cạnh EF=>\(DH\perp EF\)tại H
c.xét\(\Delta DMH\)và\(\Delta DNH\)có
DM=DN(GT)
HM=HN(GT)
DM:chung
=>\(\Delta DMH=\Delta DNH\left(c-c-c\right)\)
=>\(\widehat{DMH}=\widehat{DNH}\)(hai góc tương ứng)
Cho hình thang vuông ABCD tại A và D. Gọi E,F lần lượt là trung điểm của AD,BC.
Chứng minh:
a) ADFcân tại F b) \(\widehat{BAF}=\widehat{CDF}\)
Hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AB//CD
mà AB\(\perp\)AD
nên EF\(\perp\)AD
Xét ΔFAD có
FE là đường cao ứng với cạnh AD
FE là đường trung tuyến ứng với cạnh AD
Do đó: ΔFAD cân tại F
b) Ta có: \(\widehat{BAF}+\widehat{DAF}=90^0\)
\(\widehat{CDF}+\widehat{FDA}=90^0\)
mà \(\widehat{FAD}=\widehat{FDA}\)(ΔFAD cân tại F)
nên \(\widehat{BAF}=\widehat{CDF}\)