a: Phương trình hoành độ giao điểm là: \(x^2-mx+m-1=0\)

\(\Delta=\left(-m\right)^2-4\cdot\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2\)

Để (P) cắt (d) tại hai điểm phân biệt thì m-2<>0

hay m<>2

b: \(\left|x_A-x_B\right|< 3\)

\(\Leftrightarrow\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}< 3\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2< 9\)

\(\Leftrightarrow m^2-4\left(m-1\right)< 9\)

\(\Leftrightarrow\left(m-2\right)^2-3< 0\)

=>(m+1)(m-5)<0

=>-1<m<5

a. Em tự giải

b.

Phương trình hoành độ giao điểm (d) và (P):

\(x^2=\left(m+2\right)x-m+3\Leftrightarrow x^2-\left(m+2\right)x+m-3=0\)

\(\Delta=\left(m+2\right)^2-4\left(m-3\right)=m^2+16>0;\forall m\)

(d) cắt (P) tại 2 điểm phân biệt với mọi m

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1x_2=m-3\end{matrix}\right.\)

\(x_1^2+x_2^2+x_1x_2\le5\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-x_1x_2\le5\)

\(\Leftrightarrow\left(m+2\right)^2-\left(m-3\right)\le5\)

\(\Leftrightarrow m^2+3m+2\le0\)

\(\Leftrightarrow\left(m+1\right)\left(m+2\right)\le0\)

\(\Rightarrow-2\le m\le-1\)

a: khi m=3 thì (d): y=5x

PTHĐGĐ là:

x^2=5x

=>x=0 hoặc x=5

=>y=0 hoặc y=25

b:

PTHĐGĐ là:

x^2-(m+2)x+m+3=0

Δ=(m+2)^2-4(m+3)

=m^2+4m+4-4m-12=m^2-8

Để (d) cắt (P) tại 2 điểm pb thì m^2-8>0

=>m>2 căn 2 hoặc m<-2 căn 2

x1^2+x2^2+x1x2<=5

=>(x1+x2)^2-x1x2<=5

=>(m+2)^2-m-3<=5

=>m^2+4m+4-m-3-5<=0

=>m^2+3m-4<=0

=>(m+4)(m-1)<=0

=>-4<=m<=1

a: PTHĐGĐ là:

x^2+mx-m-2=0(1)

Khi m=2 thì (1) sẽ là

x^2+2x-2-2=0

=>x^2+2x-4=0

=>\(\left[{}\begin{matrix}x=-1+\sqrt{5}\\x=-1-\sqrt{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=6-2\sqrt{5}\\y=6+2\sqrt{5}\end{matrix}\right.\)

b: Δ=m^2-4(-m-2)

=m^2+4m+8

=(m+2)^2+4>0 với mọi x

=>(d) luôn cắt (P) tại hai điểm phân biệtx

x1^2+x2^2=7

=>(x1+x2)^2-2x1x2=7

=>(-m)^2-2(-m-2)=7

=>m^2+2m+4-7=0

=>m^2+2m-3=0

=>m=-3 hoặc m=1

b) Phương trình hoành độ giao điểm của (P) và (d) là:

- x 2  = 2mx - 5 ⇔  x 2  + 2mx - 5 = 0

Δ'= m 2 + 5 > 0 với ∀m ∈ R

Vậy trên mặt phẳng Oxy đường thẳng (d) và Parabol (P) luôn cắt nhau tại hai điểm phân biệt.

Khi m = 2, phương trình hoành độ giao điểm của (P) và (d) là:

- x 2 = 4x - 5 ⇔ x 2  + 4x - 5 = 0

Δ = 4 2  - 4.1.(-5) = 36

⇒ Phương trình có 2 nghiệm

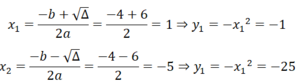
Vậy tọa độ hai giao điểm là M(1;-1) và N(-5;-25)

a: PTHĐGĐ là:

x^2-4x+4m^2+1=0

Δ=(-4)^2-4(4m^2+1)

=16-16m^2-4=-16m^2+12

Để (d) cắt (P) tại hai điểm phân biệt thì -16m^2+12>0

=>-16m^2>-12

=>m^2<3/4

=>\(-\dfrac{\sqrt{3}}{2}< m< \dfrac{\sqrt{3}}{2}\)

b: x1,x2 nguyên

=>x1+x2 nguyên và x2*x1 nguyên

=>4 nguyên và 4m^2+1 nguyên

=>4m^2 nguyên

=>m^2 nguyên

=>\(m=k^2\left(k\in Z\right)\)

b: Thay m=2 vào (d), ta được:

y=2x-2+1=2x-1

Phương trình hoành độ giao điểm là:

\(x^2=2x-1\)

=>\(x^2-2x+1=0\)

=>(x-1)^2=0

=>x-1=0

=>x=1

Thay x=1 vào (P), ta được:

\(y=1^2=1\)

Vậy: Khi m=2 thì (P) cắt (d) tại A(1;1)

b: Phương trình hoành độ giao điểm là:

\(x^2=2x-m+1\)

=>\(x^2-2x+m-1=0\)

\(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot\left(m-1\right)\)

=4-4m+4

=-4m+8

Để (P) cắt (d) tại hai điểm phân biệt thì Δ>0

=>-4m+8>0

=>-4m>-8

=>m<2

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)

y1,y2 thỏa mãn gì vậy bạn?

b) Phương trình hoành độ giao điểm của (P) và (d) là:

\(x^2=2\left(m-1\right)x+5-2m\)

\(\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0\)

Áp dụng hệ thức Vi-et, ta được:

\(x_1+x_2=2\left(m-1\right)\)

Ta có: \(x_1+x_2=6\)

\(\Leftrightarrow2\left(m-1\right)=6\)

\(\Leftrightarrow m-1=3\)

hay m=4

Vậy: m=4

Phương trình hoành độ giao điểm:

\(-\dfrac{1}{2}x^2=mx+m-3\Leftrightarrow x^2+2mx+2m-6=0\) (1)

a. Khi \(m=-1\), (1) trở thành:

\(x^2-2x-8=0\Rightarrow\left[{}\begin{matrix}x=4\Rightarrow y=-8\\x=-2\Rightarrow y=-2\end{matrix}\right.\)

Vậy (d) cắt (P) tại 2 điểm có tọa độ là \(\left(4;-8\right)\) ; \(\left(-2;-2\right)\)

b. 

\(\Delta'=m^2-2m+6=\left(m+1\right)^2+5>0;\forall m\Rightarrow\left(1\right)\) có 2 nghiệm pb với mọi m

Hay (d) cắt (P) tại 2 điểm pb với mọi m

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)

\(x_1^2+x_2^2=14\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=14\)

\(\Leftrightarrow4m^2-2\left(2m-6\right)=14\)

\(\Leftrightarrow4m^2-4m-2=0\Rightarrow m=\dfrac{1\pm\sqrt{3}}{2}\)