Trong các khẳng định sau, khẳng định nào đúng?
A. Hai tam giác đồng dạng thì bằng nhau.
B. Hai tam giác bằng nhau thì đồng dạng.
C. Hai tam giác bằng nhau thì không đồng dạng.
D. Hai tam giác cân thì luôn đồng dạng
Bài tập cuối chương VIII
Bài 1 (SGK Chân trời sáng tạo trang 84)
Thảo luận (1)
Bài 2 (SGK Chân trời sáng tạo trang 84)
Nếu \(\Delta ABC\backsim\Delta MNP\) theo tỉ số \(k = 3\) thì \(\Delta MNP\backsim\Delta ABC\) theo tỉ số
A. \(\frac{1}{3}\).
B. \(\frac{1}{9}\).
C. \(3\).
D. \(9\).
Thảo luận (1)Hướng dẫn giảiĐáp án đúng là A
Vì \(\Delta ABC\backsim\Delta MNP\) theo tỉ số \(k = 3\) nên \(\Delta MNP\backsim\Delta ABC\) theo tỉ số \(\frac{1}{3}\).
(Trả lời bởi Hà Quang Minh)
Bài 3 (SGK Chân trời sáng tạo trang 84)
Nếu \(\Delta ABC\)có \(MN//AB\) (với \(M \in AC,N \in BC\)) thì
A. \(\Delta CMN\backsim\Delta ABC\).
B. \(\Delta CNM\backsim\Delta CAB\).
C. \(\Delta CNM\backsim\Delta ABC\).
D. \(\Delta MNC\backsim\Delta ABC\).
Thảo luận (1)Hướng dẫn giảiĐáp án đúng là D
Vì \(MN//AB\) và \(M \in AC,N \in BC\) nên \(\Delta MNC\backsim\Delta ABC\).
(Trả lời bởi Kiều Sơn Tùng)
Bài 4 (SGK Chân trời sáng tạo trang 84)
Cho \(\Delta ABD\backsim\Delta DEF\)với tỉ số đồng dạng \(k = \frac{1}{3}\), biết \(AB = 9cm\). Khi đó, \(DE\) bằng
A. 6 cm.
B. 12 cm.
C. 3 cm.
D. 27 cm.
Thảo luận (1)Hướng dẫn giảiĐáp án đúng là D
Vì \(\Delta ABD\backsim\Delta DEF\) với tỉ số đồng dạng là \(k = \frac{1}{3}\) nên \(\frac{{AB}}{{DE}} = \frac{{AD}}{{DF}} = \frac{{BD}}{{EF}} = \frac{1}{3}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Do đó, \(\frac{{AB}}{{DE}} = \frac{1}{3} \Rightarrow \frac{9}{{DE}} = \frac{1}{3} \Rightarrow DE = \frac{{9.3}}{1} = 27\)
Vậy \(DE = 27cm.\)
(Trả lời bởi Hà Quang Minh)
Bài 5 (SGK Chân trời sáng tạo trang 84)
Nếu tam giác \(ABC\) và tam giác \(EFG\) có \(\widehat A = \widehat E;\widehat B = \widehat F\) thì
A. \(\Delta ABC\backsim\Delta EGF\).
B. \(\Delta ABC\backsim\Delta EFG\).
C. \(\Delta ACB\backsim\Delta GFE\).
D. \(\Delta CBA\backsim\Delta FGE\).
Thảo luận (1)Hướng dẫn giảiĐáp án đúng là B
Xét tam giác \(ABC\) và tam giác \(EFG\) có:
\(\widehat A = \widehat E;\widehat B = \widehat F\) (giả thuyết)
Suy ra, \(\Delta ABC\backsim\Delta EFG\)(g.g)
(Trả lời bởi Hà Quang Minh)
Bài 6 (SGK Chân trời sáng tạo trang 84)
Cho \(\Delta XYZ\backsim\Delta EFG\), biết \(XY = 6cm;EF = 8cm;EG = 12cm\). Khi đó \(XZ\) bằng
A. 10 cm.
B. 9 cm.
C. 12 cm.
D. 16 cm.
Thảo luận (1)Hướng dẫn giảiĐáp án đúng là B
Vì \(\Delta XYZ\backsim\Delta EFG\) nên \(\frac{{XY}}{{EF}} = \frac{{XZ}}{{EG}}\)(các cặp cạnh tương ứng có cùng tỉ lệ).
Thay số, \(\frac{6}{8} = \frac{{XZ}}{{12}} \Rightarrow XZ = \frac{{6.12}}{8} = 9\).
Vậy \(XZ = 9cm\).
(Trả lời bởi Hà Quang Minh)
Bài 7 (SGK Chân trời sáng tạo trang 84)
Cho \(\Delta ABC\backsim\Delta DEF\), biết \(\widehat A = 85^\circ ,\widehat B = 60^\circ \). Khi đó số đo \(\widehat F\) bằng
A.\(60^\circ \).
B. \(85^\circ \).
C. \(35^\circ \).
D. \(45^\circ \).
Thảo luận (2)Hướng dẫn giảiĐáp án đúng là C
Vì \(\Delta ABC\backsim\Delta DEF\) nên \(\widehat A = \widehat D;\widehat B = \widehat E;\widehat C = \widehat F\).
Xét tam giác \(ABC\) có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác).
Thay số, \(85^\circ + 60^\circ + \widehat C = 180^\circ \Rightarrow \widehat C = 180^\circ - 60^\circ - 85^\circ = 35^\circ \)
Vì \(\widehat C = \widehat F\) nên \(\widehat F = 35^\circ \).
(Trả lời bởi Hà Quang Minh)
Bài 8 (SGK Chân trời sáng tạo trang 84)
Cho hình thang \(ABCD\left( {AB//CD} \right)\), có hai đường chéo \(AC\) và \(DB\) cắt nhau tại \(O\). Biết \(AB = 8cm,CD = 20cm\). Khi đó \(\Delta AOB\backsim\Delta COD\) với tỉ số đồng dạng là
A.\(k = \frac{2}{3}\).
B. \(k = \frac{3}{2}\).
C. \(k = \frac{2}{5}\).
D. \(k = \frac{5}{2}\).
Thảo luận (1)Hướng dẫn giảiĐáp án đúng là C
Vì \(ABCD\) và \(AB//CD\) nên \(\widehat {OAB} = \widehat {OCD}\) (hai góc ở vị trí so le trong)
Xét tam giác \(AOB\) và tam giác \(COD\) có:
\(\widehat {OAB} = \widehat {OCD}\) (chứng minh trên)
\(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)
Suy ra, \(\Delta AOB\backsim\Delta COD\) (g.g)
Suy ra, tỉ số đồng dạng \(k = \frac{{AB}}{{CD}} = \frac{8}{{20}} = \frac{2}{5}\).
(Trả lời bởi Kiều Sơn Tùng)
Bài 9 (SGK Chân trời sáng tạo trang 85)
Trong Hình 1, cho biết \(\widehat {ABD} = \widehat {ACD},AC = 9cm,AD = 4cm\).
a) Chứng minh tam giác \(\Delta ABD\backsim\Delta ACB\).
b) Tính độ dài cạnh \(AB\).
Thảo luận (1)Hướng dẫn giảia) Xét tam giác \(ABD\) và tam giác \(ACB\) có:
\(\widehat {ABD} = \widehat {ACB}\) (giả thuyết)
\(\widehat A\) chung
Suy ra, \(\Delta ABD\backsim\Delta ACB\) (g.g)
b) Vì \(\Delta ABD\backsim\Delta ACB\)
Suy ra, \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Suy ra, \(A{B^2} = AC.AD = 9.4 = 36 \Rightarrow AB = \sqrt {36} = 6\)
Vậy \(AB = 6cm.\)
(Trả lời bởi Hà Quang Minh)
Bài 10 (SGK Chân trời sáng tạo trang 85)
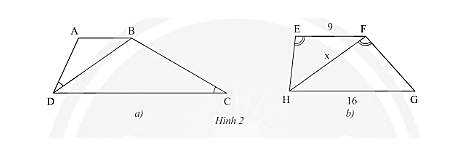
a) Cho hình thang \(ABCD\left( {AB//CD} \right)\), biết \(\widehat {ADB} = \widehat {DCB}\) (Hình 2a).
Chứng minh rằng \(B{D^2} = AB.CD\).
b) Cho hình thang \(EFGH\left( {FF//GH} \right),\widehat {HEF} = \widehat {HFG},EF = 9m,GH = 16m\) (Hình 2b).
Tính độ dài \(x\) của \(HF\).
Thảo luận (1)Hướng dẫn giảia) Vì \(ABCD\) là hình thang có \(AB//CD\) nên \(\widehat {ABD} = \widehat {BDC}\) (hai góc so le trong)
Xét tam giác \(ABD\) và tam giác \(BDC\) có:
\(\widehat {ADB} = \widehat {DCB}\) (giả thuyết)
\(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên)
Suy ra, \(\Delta ABD\backsim\Delta BDC\) (g.g)
Suy ra, \(\frac{{AB}}{{BD}} = \frac{{BD}}{{CD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(B{D^2} = AB.CD\).
b) Vì \(EFGH\) là hình thang có \(FF//GH\)nên \(\widehat {EFH} = \widehat {FHG}\) (hai góc so le trong)
Xét tam giác \(EFH\) và tam giác \(FHG\) có:
\(\widehat {HEF} = \widehat {HFG}\) (giả thuyết)
\(\widehat {EFH} = \widehat {FHG}\) (chứng minh trên)
Suy ra, \(\Delta EFH\backsim\Delta FHG\) (g.g)
Suy ra, \(\frac{{EF}}{{FH}} = \frac{{FH}}{{HG}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(F{H^2} = EF.HG = 9.16 = 144 \Rightarrow FH = \sqrt {144} = 12\).
Vậy \(FH = 12cm\).
(Trả lời bởi Hà Quang Minh)