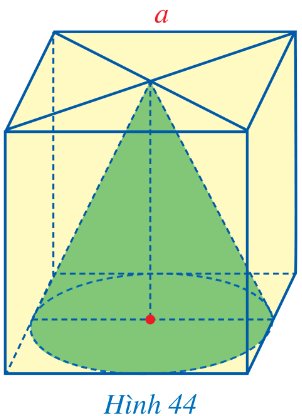
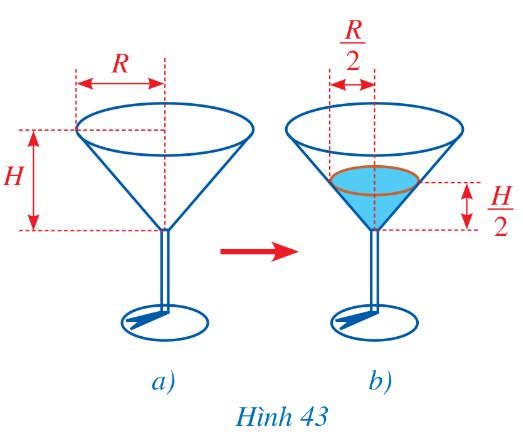
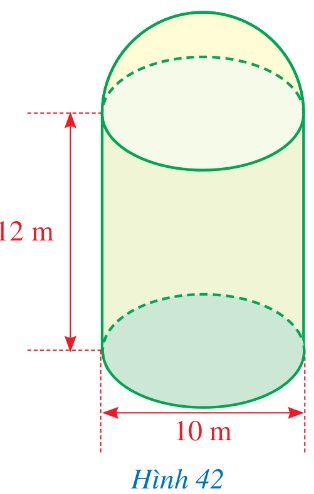
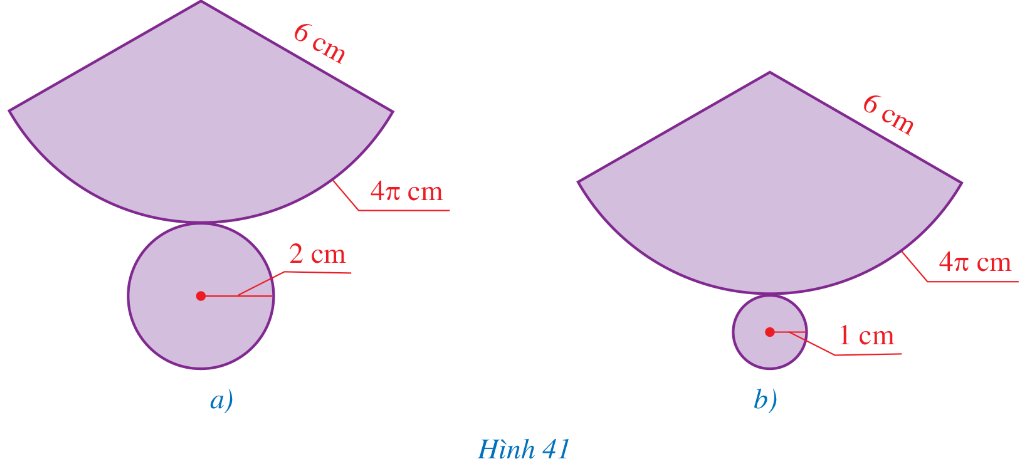
Có một quả bóng rổ (loại số 7 cho nam) và một quả bóng tennis (Hình 45). Biết rằng diện tích bề mặt của quả bóng rổ khoảng 1 884,75 cm2 và bán kính của quả bóng rổ gấp khoảng 2 lần đường kính của quả bóng tennis. Hỏi diện tích bề mặt của quả bóng tennis đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần mười)?