Theo dõi nhiệt độ trung bình hàng năm của hai thành phố A và B từ năm 1956 đến năm 1957 (đo theo độ C) người ta lập được bảng như sau :
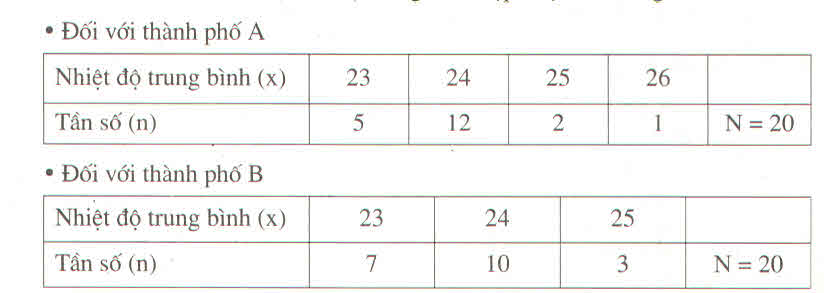
Hãy so sánh nhiệt độ trung bình hàng năm giữa hai thành phố ?
Theo dõi nhiệt độ trung bình hàng năm của hai thành phố A và B từ năm 1956 đến năm 1957 (đo theo độ C) người ta lập được bảng như sau :

Hãy so sánh nhiệt độ trung bình hàng năm giữa hai thành phố ?
Hai xạ thủ A và B cùng bắn 20 phát đạn, kết quả được ghi lại dưới đây :

Thảo luận (3)Hướng dẫn giảiĐiểm trung bình của xạ thủ A.
Giá trị (x)
Tần số (n)
Các tích (x.n)
8
5
40
9
6
54
10
9
90
N = 20
Tổng: 184
¯¯¯¯¯X=18420=9,2X¯=18420=9,2 Điểm trung bình của xạ thủ B.
Giá trị (x)
Tần số (n)
Các tích (x.n)
6
2
12
7
1
7
9
5
45
10
12
120
N = 20
Tổng: 184
¯¯¯¯¯X=18420=9,2
Khả năng của từng người là như nhau
(Trả lời bởi Nguyễn Thị Diễm Quỳnh)
Đo chiều cao của 100 học sinh lớp 6 (đơn vị đo : cm) và được kết quả theo bảng 26 :
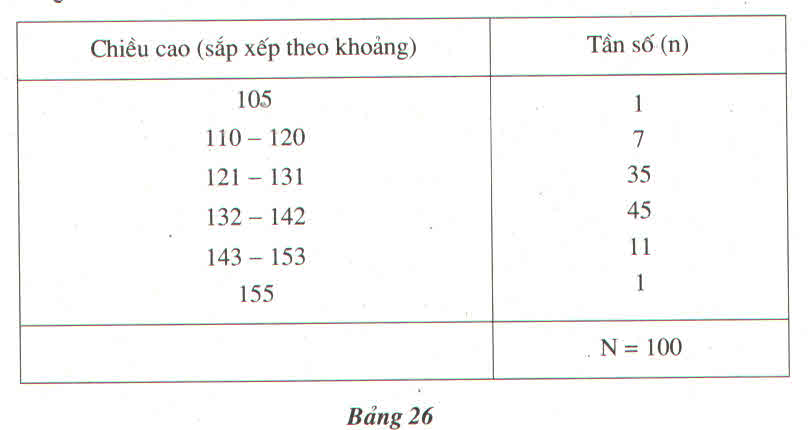
a) Bảng này có gì khác so với những bảng "tần số" đã biết ?
b) Ước tính số trung bình cộng trong trường hợp này ?
Thảo luận (2)Hướng dẫn giảia) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.
Số trung bình cộng:\(\overline{X}=\dfrac{105+805+4410+6165+1628+155}{100}=132,68\left(cm\right)\)
(Trả lời bởi Hiiiii~)

Thảo luận (2)Hướng dẫn giải
Giá trị (x) Tần số (n) Các tích (x.n) 17 3 51 18 5 90 19 4 76 20 2 40 21 3 63 22 2 44 24 3 72 26 3 78 28 1 28 30 1 30 31 2 62 32 1 32 = \(\dfrac{666}{30}=22,2\)
N = 30 Tổng: 666 (Trả lời bởi Dương Nguyễn)
Đo chiều cao của 100 học sinh lớp 6 (đơn vị đo : cm) và được kết quả theo bảng 26 :

a) Bảng này có gì khác so với những bảng "tần số" đã biết ?
b) Ước tính số trung bình cộng trong trường hợp này ?
Thảo luận (1)Hướng dẫn giảia) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.
Số trung bình cộng:
\(\overline{X}=\dfrac{105+805+4410+6165+1628+155}{100}=132,68\left(cm\right)\)
(Trả lời bởi Lưu Hạ Vy)
Theo dõi thời gian làm một bài toán (tính bằng phút) của 50 học sinh, thầy giáo lập được bảng 25 :
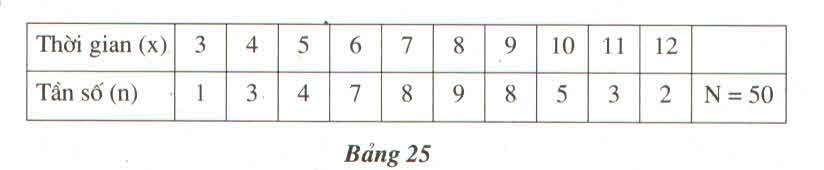
a) Tính số trung bình cộng
b) Tìm mốt của dấu hiệu
Thảo luận (1)Hướng dẫn giảia) Số trung bình cộng về thời gian làm một bài toán của 50 học sinh.
b) Tần số lớn nhất là 9, giá trị ứng với tần số 9 là 8. Vậy Mốt của dấu hiệu: Mo = 8 (phút).
(Trả lời bởi Lưu Hạ Vy)
Để nghiên cứu "tuổi thọ" của một loại bóng đèn, người ta đã chọn tùy ý 50 bóng và bật sáng liên tục cho tới lúc chúng tự tắt. "Tuổi thọ" của các bóng (tính theo giờ) được ghi lại ở bảng 23 (làm tròn đến hàng chục) "

a) Dấu hiệu cần tìm hiểu ở đây là gì và số các giá trị là bao nhiêu ?
b) Tính số trung bình cộng ?
c) Tìm mốt của dấu hiệu ?
Thảo luận (2)Hướng dẫn giảia) - Dấu hiệu: Thời gian cháy sáng liên tục cho tới lúc tự tắt của bóng đèn tức "tuổi thọ" của một loại bóng đèn.
- Số các giá trị N = 50
b) Số trung bình cộng của tuổi thọ các bóng đèn đó là:
c) Tìm mốt của dấu hiệu:
Ta biết mốt là giá trị có tần số lớn nhất trong bảng. Mà tần số lớn nhất trong bảng là 18.
Vậy mốt của dấu hiệu bằng 1180 hay Mo = 1180.
(Trả lời bởi Lưu Hạ Vy)
Hãy tính số trung bình cộng của dấu hiệu ở bài tập 9 ?
Thảo luận (1)Hướng dẫn giảiBảng "tần số" ở bài tập 9 viết theo cột:
Vậy số trung bình cộng \(\overline{X}\) là \(\overline{X}=\dfrac{254}{35}\approx7,26\)
(Trả lời bởi Lưu Hạ Vy)
Quan sát bảng "tần số" (bảng 24) và cho biết có nên dùng số trung bình cộng làm "đại diện" cho dấu hiệu không ? Vì sao ?
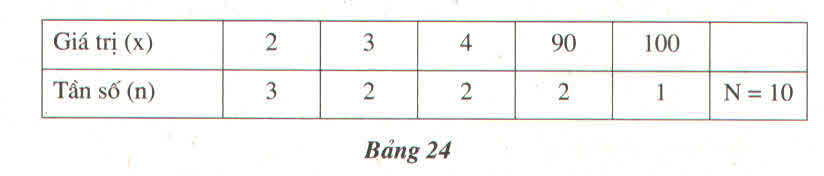
Thảo luận (1)Hướng dẫn giảiTa có số trung bình cộng của các giá trị trong bảng là:
Số trung bình cộng này không làm "đại diện" cho dấu hiệu vì chênh lệch quá lớn so với 2; 3; 4. Các giá trị khác nhau của dấu hiệu hiện có khoảng chênh lệch rất lớn 2, 3, 4 so với 100, 90.
(Trả lời bởi Lưu Hạ Vy)
Số cân nặng (tính bằng kg) của 120 em của một trường mẫu giáo ở thành phố A được ghi lại trong bảng 27 :
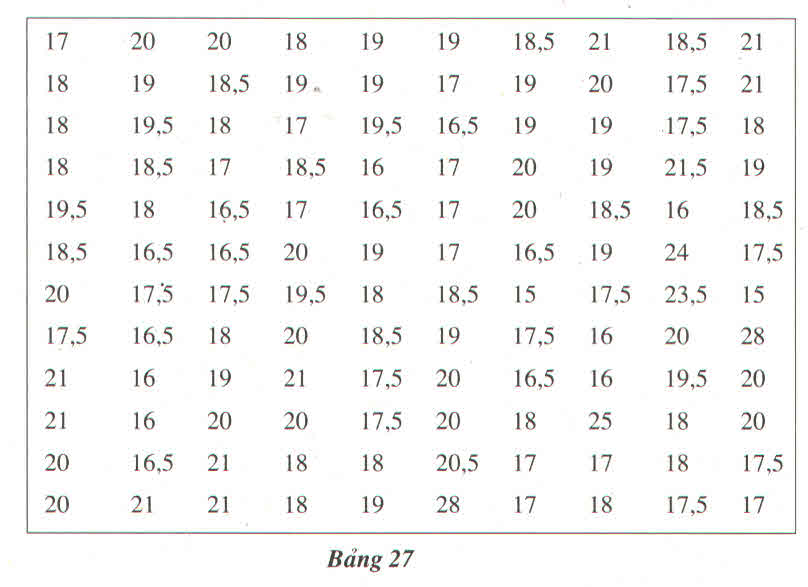
Hãy tính số trung bình cộng (có thể sử dụng máy tính bỏ túi) ?
Thảo luận (3)Hướng dẫn giải