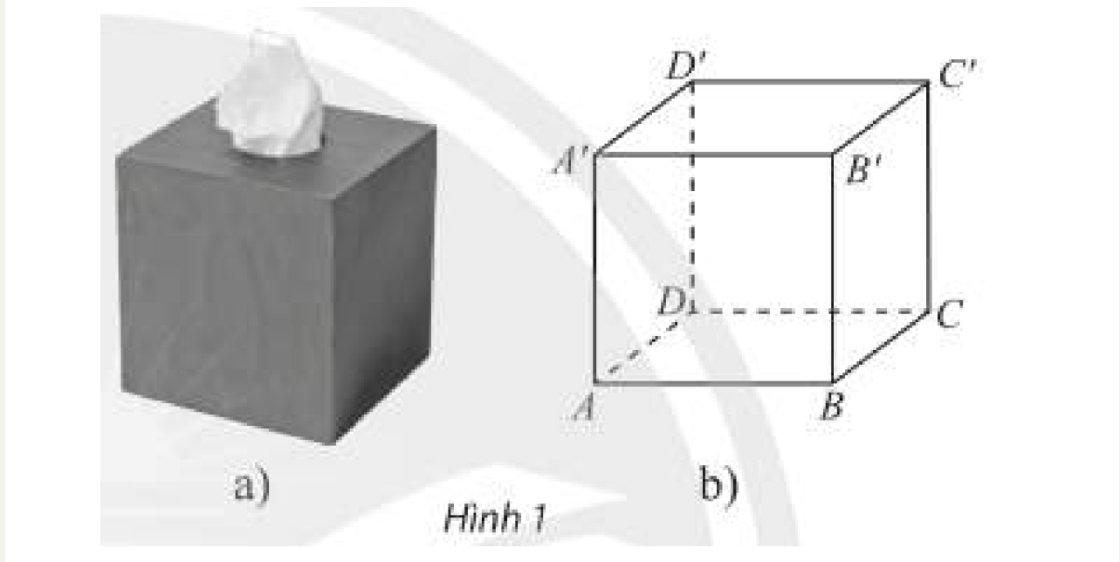
Hộp giấy có các mặt là hình vuông ở Hình 1a được vẽ lại với các đỉnh là \(A,B,C,D,A',B',C',D'\) như Hình 1b. Gọi tên cặp mặt phẳng:
a) Có ba điểm chung không thẳng hàng.
b) Là hai mặt phẳng phân biệt và có một điểm chung.
c) Không có bất kì điểm chung nào.