Ở tiểu học, các em đã nhận biết được một số vật thể có dạng hình cầu, như ở Hình 28.

Hình cầu có những đặc điểm gì?
Ở tiểu học, các em đã nhận biết được một số vật thể có dạng hình cầu, như ở Hình 28.

Hình cầu có những đặc điểm gì?
Cắt một miếng bìa có dạng nửa hình tròn (đường kính AB = 2R, tâm O). Khi quay miếng bìa một vòng quanh đường thẳng cố định chứa đường kính AB (Hình 29a), miếng bìa đó tạo nên một hình như ở Hình 29b. Hình đó có dạng hình gì?
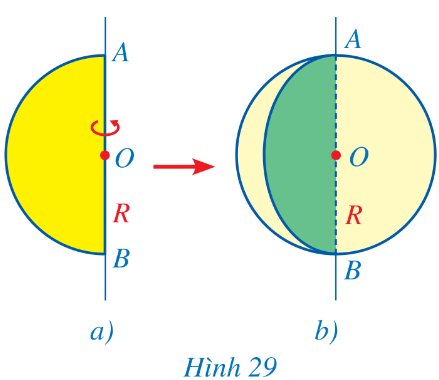
Thảo luận (1)Hướng dẫn giảiHình được tạo ra khi quay một nửa đường tròn một vòng quanh đường thẳng cố định chứa đường kính AB là một hình cầu.
(Trả lời bởi Nguyễn Quốc Đạt)
Cắt một số miếng bìa có dạng hình tròn có cùng đường kính. Mỗi miếng bìa tròn đó được cắt làm hai nửa hình tròn. Ghép các miếng bìa có dạng nửa hình tròn đó để được một hình cầu như ở Hình 31.
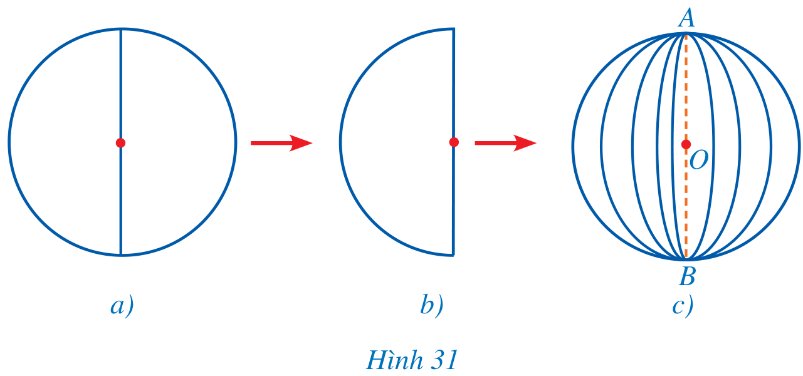
Thảo luận (1)Hướng dẫn giảiLàm theo hướng dẫn để cắt dán được hình cầu như Hình 31c.
(Trả lời bởi Nguyễn Quốc Đạt)
Tạo lập một hình cầu có bán kính là 3 cm.
Thảo luận (1)Hướng dẫn giảiBước 1: Cắt một số miếng bìa có dạng hình tròn có cùng bán kính 3cm.
Bước 2: Mỗi miếng bìa tròn đó được cắt làm hai nửa hình tròn.
Bước 3: Ghép các miếng bìa có dạng nửa hình tròn đó để được một hình cầu bán kính 3cm.
(Trả lời bởi Nguyễn Quốc Đạt)
a) Chuẩn bị một quả cam có dạng hình cầu. Dùng dao để cắt nó thành hai phần. Phần mặt cắt của quả cam như ở Hình 32 có dạng hình gì?

b) Quan sát Hình 33 và cho biết một mặt phẳng cắt một hình cầu sẽ tạo ra hình gì?
Thảo luận (1)Hướng dẫn giảia) Mặt cắt của quả cam có dạng hình tròn.
b) Một mặt phẳng cắt một hình cầu sẽ tạo ra hình tròn.
(Trả lời bởi Nguyễn Quốc Đạt)
Thực hiện các hoạt động sau:
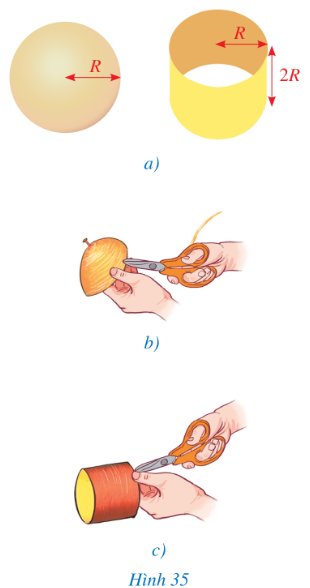
a) Chuẩn bị một mặt cầu bằng nhựa (chẳng hạn quả bóng bằng nhựa mỏng) có bán kính là R và một hình trụ bằng bìa cứng (hoặc nhựa mỏng) có bán kính đáy là R và chiều cao là 2R (như Hình 35a); một cuộn dây mảnh, không dãn (chẳng hạn dây len) đủ dài.
b) Dùng cuộn dây đó cuốn dần dần để phủ kín một nửa mặt cầu rồi cắt dây ở điểm cuối cùng (Hình 35b). Như vậy, đoạn dây thứ nhất “đã lát kín” một nửa mặt cầu. Tiếp tục dùng cuộn dây đó cuốn dần dần để phủ kín mặt xung quanh của hình trụ và cắt dây ở điểm cuối cùng (Hình 35c). Ta được đoạn dây thứ hai “lát kín” mặt xung quanh của hình trụ đã cho.
Gỡ từng đoạn dây quấn quanh nửa mặt cầu và mặt xung quanh của hình trụ nói trên, ta thấy hai đoạn dây đó có độ dài bằng nhau.
Do hai đoạn dây lần lượt lát kín một nửa mặt cầu, mặt xung quanh của hình trụ và độ dài hai đoạn dây đó bằng nhau nên ta có thể coi hai mặt đó có diện tích bằng nhau.
c) Tính diện tích xung quanh của hình trụ có bán kính đáy là R và chiều cao là 2R. Từ đó, hãy nêu dự đoán về công thức tính diện tích của mặt cầu bán kính R.
Thảo luận (1)Hướng dẫn giảia) Chuẩn bị các vật thể: quả bóng bàn, hình trụ theo kích thước của quả bóng, cuộn dây.
b) Đánh dấu 1 nửa hình cầu, cuốn dây để lát kính nửa mặt cầu đó.
Dùng đoạn dây khác lát kín mặt xung quanh của hình trụ.
Gỡ 2 đoạn dây đó và thấy độ dài 2 đoạn dây bằng nhau nên hai mặt đó có diện tích bằng nhau.
c) Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .R.2R = 4\pi {R^2}.\)
Vì diện tích xung quanh của hình trụ bằng diện tích mặt cầu nên diện tích mặt cầu là \(S = 4\pi {R^2}.\)
(Trả lời bởi Nguyễn Quốc Đạt)
Một quả bóng đá theo tiêu chuẩn chuyên nghiệp (cho cả nam và nữ, từ khoảng 11, 12 tuổi trở lên), thường nặng khoảng 450 g, có chu vi đường tròn lớn khoảng 70 cm. Diện tích bề mặt của quả bóng đá như thế bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm)?
Thảo luận (1)Hướng dẫn giảiTa có: \(C = \pi 2R\) nên bán kính quả bóng là:
\(R = \frac{C}{{2\pi }} = \frac{{70}}{{2\pi }} = \frac{{35}}{\pi }\left( {cm} \right).\)
Diện tích bề mặt quả bóng là:
\(S = 4\pi {R^2} = 4\pi {\frac{{35}}{{{\pi ^2}}}^2} \approx 1560,51\left( {c{m^2}} \right).\)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho một hình cầu bán kính R và một cốc thuỷ tinh có dạng hình trụ với bán kính đáy là R, chiều cao là 2R.
Đặt hình cầu nằm khít trong cốc hình trụ rồi đổ đầy nước vào cốc đó (Hình 36a). Nhấc nhẹ hình cầu ra khỏi cốc. Đo độ cao cột nước còn lại, ta thấy độ cao này chỉ bằng \(\dfrac{1}{3}\) chiều cao của cốc (Hình 36b).
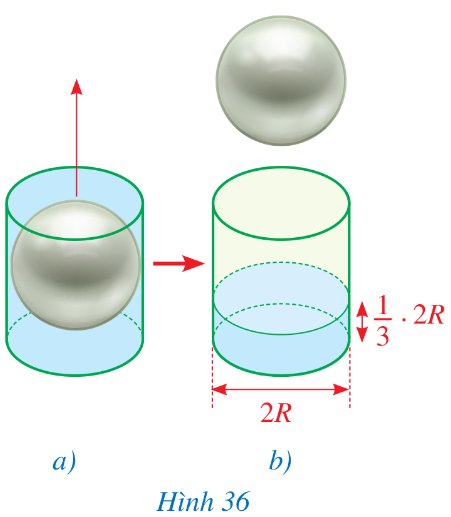
Hãy cho biết thể tích của hình cầu bằng bao nhiêu phần thể tích của cốc hình trụ.
Thảo luận (1)Hướng dẫn giảiThể tích của cốc hình trụ là:
\(\pi .{R^2}.2R = 2\pi .{R^3}\)
Khi bỏ quả cầu ra thì độ cao nước còn lại bằng \(\frac{1}{3}\) chiều cao của cốc nên chiều cao nước là: \(\frac{1}{3}.2R = \frac{2}{3}R\).
Thể tích nước trong cốc là:
\(\pi .{R^2}.\frac{2}{3}R = \frac{2}{3}\pi {R^3}\).
Thể tích của cốc hình trụ chính là tổng thể tích của hình cầu và thể tích nước trong cốc.
Suy ra thể tích của hình cầu là:
\(2\pi {R^3} - \frac{2}{3}\pi {R^3} = \left( {2 - \frac{2}{3}} \right)\pi {R^3} = \frac{4}{3}\pi {R^3}\).
Vậy thể tích của hình cầu bằng \(\frac{{\frac{4}{3}\pi {R^3}}}{{2\pi {R^3}}} = \frac{2}{3}\) phần thể tích của hình trụ.
(Trả lời bởi Nguyễn Quốc Đạt)
Trong những vật thể ở các hình 37a, 37b, 37c, 37d, 37e, vật thể ở hình nào có dạng hình cầu?
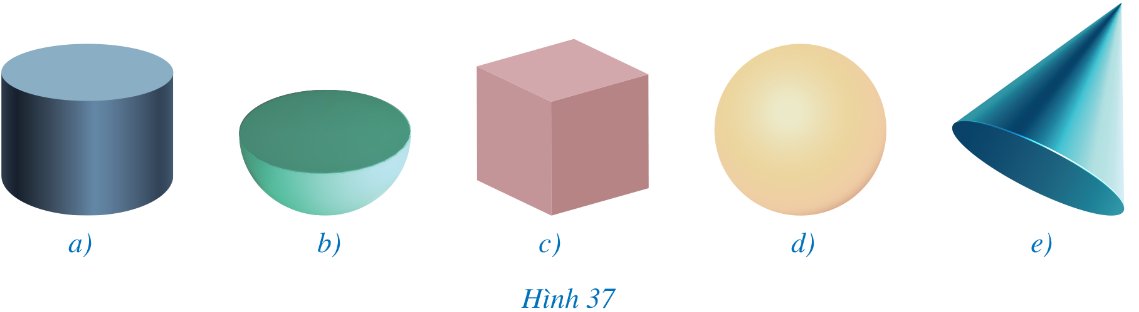
Thảo luận (1)Hướng dẫn giảiVật thể ở hình 37d có dạng hình cầu.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho một mặt phẳng đi qua tâm O của một hình cầu (Hình 38).
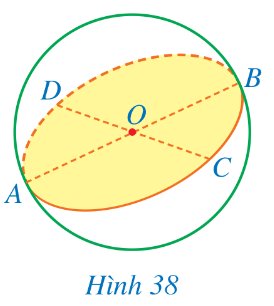
Quan sát Hình 38, hãy chỉ ra:
a) Hai đường kính của hình cầu;
b) Bốn bán kính của hình cầu;
c) Một hình tròn lớn của hình cầu.
Thảo luận (1)Hướng dẫn giảia) Hai đường kính của hình cầu: AB, CD;
b) Bốn bán kính của hình cầu: OA, OB, OC, OD;
c) Một hình tròn lớn của hình cầu: (O, OA).
(Trả lời bởi Nguyễn Quốc Đạt)