Tìm các tiệm cận của đồ thị hàm số sau:
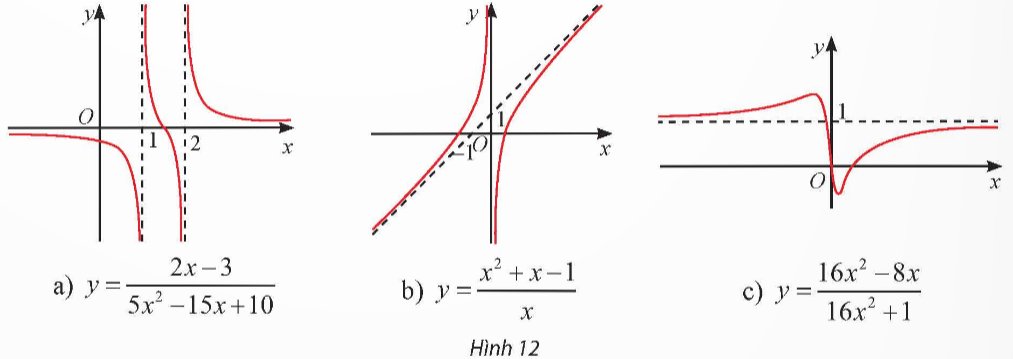
Tìm các tiệm cận của đồ thị hàm số sau:

Nồng độ oxygen trong hồ theo thời gian t cho bởi công thức \(y\left(t\right)=5-\dfrac{15t}{9t^2+1}\), với y được tính theo mg/l và t được tính theo giờ, t ≥ 0. Tìm các đường tiệm cận của đồ thị hàm số y = y(t). Từ đó, có nhận xét gì về nồng độ oxygen trong hồ khi thời gian t trở nên rất lớn.
Thảo luận (1)Hướng dẫn giảiXét \(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\)
Ta có: \(\mathop {\lim }\limits_{t \to + \infty } y(t) = \mathop {\lim }\limits_{t \to + \infty } (5 - \frac{{15t}}{{9{t^2} + 1}}) = \mathop {\lim }\limits_{t \to + \infty } \frac{{45{t^2} - 15t + 5}}{{9{t^2} + 1}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{45 - \frac{{15}}{t} + \frac{5}{{{t^2}}}}}{{9 + \frac{1}{{{t^2}}}}} = 5\)\(\mathop {\lim }\limits_{t \to - \infty } y(t) = \mathop {\lim }\limits_{t \to - \infty } (5 - \frac{{15t}}{{9{t^2} + 1}}) = \mathop {\lim }\limits_{t \to - \infty } \frac{{45{t^2} - 15t + 5}}{{9{t^2} + 1}} = \mathop {\lim }\limits_{t \to - \infty } \frac{{45 - \frac{{15}}{t} + \frac{5}{{{t^2}}}}}{{9 + \frac{1}{{{t^2}}}}} = 5\)
Vậy đường thẳng y = 5 là tiệm cận ngang của đồ thị hàm số
Nhận xét: Khi thời gian \(t\) trở nên rất lớn, nồng độ oxygen trong hồ tiến dần về 5mg/l
(Trả lời bởi Nguyễn Quốc Đạt)
Tìm tiệm cận của đồ thị hàm số khối lượng hạt \(m=m\left(v\right)=\dfrac{m_0}{\sqrt{1-\dfrac{v^2}{c^2}}}\) trong hoạt động khởi động (trang 19).
Thảo luận (1)Hướng dẫn giảiXét \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\)
Tập xác định: \(D = \mathbb{N}\backslash \{ c\} \)
Ta có: \(\mathop {\lim }\limits_{v \to {c^ + }} m(v) = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty \); \(\mathop {\lim }\limits_{v \to {c^ - }} m(v) = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = - \infty \)
Vậy đường thẳng x = c là tiệm cận đứng của đồ thị hàm số
(Trả lời bởi Nguyễn Quốc Đạt)