Tìm phép quay biến hình ngũ giác đều tâm I thành chính nó (Hình 8).

Tìm phép quay biến hình ngũ giác đều tâm I thành chính nó (Hình 8).

Vẽ hình vuông ABCD tâm O (Hình 5a). Cắt một tấm bìa hình vuông (gọi là H) cùng độ dài cạnh với hình vuông ABCD (Hình 5b). Đặt hình vuông H trùng khít lên hình vuông ABCD sao cho tại đỉnh M của H trùng với điểm A, rồi dùng đinh ghim cố định tâm của H tại tâm O của hình vuông ABCD (Hình 5c). Quay hình vuông H quanh điểm O ngược chiều kim đồng hồ cho đến khi đỉnh M của H trùng lại với đỉnh A (Hình 5d).
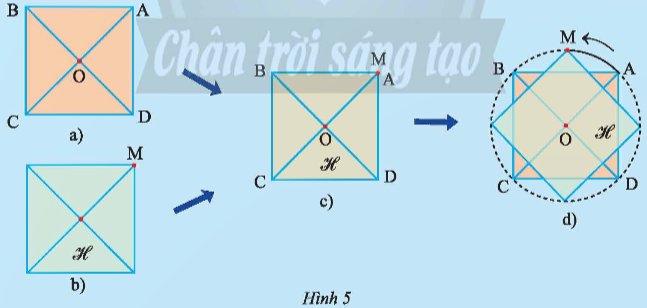
a) Khi điểm M trùng với B thì M vạch lên một cung tròn có số đo bằng bao nhiêu?
b) Trong quá trình trên, hình vuông H trùng khít với hình vuông ABCD bao nhiêu lần (không tính vị trí ban đầu trước khi quay)? Ứng với mỗi lần đó, điểm M vạch nên cung có số đo bao nhiêu?
Thảo luận (1)Hướng dẫn giảia) Khi điểm M trùng với B thì M vạch lên một cung tròn có số đo bằng 270o.
b) Trong quá trình trên, hình vuông H trùng khít với hình vuông ABCD 4 lần (không tính vị trí ban đầu trước khi quay).
- Lần 1, điểm M vạch lên cung số đo 90o.
- Lần 2, điểm M vạch lên cung số đo 180o.
- Lần 3, điểm M vạch lên cung số đo 270o.
- Lần 4, điểm M vạch lên cung số đo 360o.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho đa giác đều 9 cạnh có tâm O và AB, BC là hai cạnh đa giác (Hình 12).
a) Tìm số đo các góc \(\widehat {AOB}\), \(\widehat {ABO}\), \(\widehat {ABC}\).
b) Tìm các phép quay biến đa giác thành chính nó.

Thảo luận (1)Hướng dẫn giảia) 9 đỉnh của đa giác chia đường tròn thành 9 phần bằng nhau, số đo mỗi cung là: 360o : 9 = 40o.
Vì \(\widehat {AOB}\) là góc nội tiếp chắn cung AB nhỏ
Suy ra \(\widehat {AOB} = {40^o}\).
Do OA = OB = R nên tam giác AOB cân tại O
Suy ra \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = {70^o}\).
Tương tự, ta có \(\widehat {COB} = {40^o}\).
Suy ra \(\widehat {OBC} = \widehat {OCB} = \frac{{{{180}^o} - \widehat {BOC}}}{2} = {70^o}\)
Ta có \(\widehat {ABC} = \widehat {OBA} + \widehat {OBC} = {70^o} + {70^o} = {140^o}\).
b) Các phép quay biến đa giác thành chính nó là các phép quay 40o, 80o, 120o, 160o, 200o, 240o, 280o, 320o hoặc 360o tâm O cùng chiều hay ngược chiều kim đồng hồ.
(Trả lời bởi Nguyễn Quốc Đạt)
Một vòng quay may mắn có dạng hình đa giác đều 10 cạnh (Hình 9). Tìm các phép quay biến đa giác này thành chính nó.

Thảo luận (1)Hướng dẫn giải10 đỉnh của đa giác đều, 10 cạnh chia đường tròn thành 10 cung bằng nhau mỗi cung có số đo 36o. Từ đó, các phép quay biến đa giác đều 10 cạnh thành chính nó là các phép quay 36o, 72o, 108o, 144o, 180o, 216o, 252o, 288o, 324o, 360o; tâm đường tròn cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
(Trả lời bởi Nguyễn Quốc Đạt)
Gọi tên đa giác đều trong mỗi hình sau và tìm các phép quay có thể biến mỗi hình dưới đây thành chính nó.
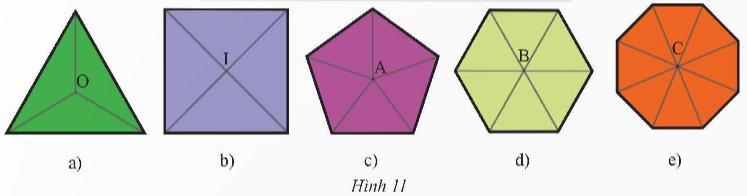
Thảo luận (1)Hướng dẫn giảia) Tam giác đều. Các phép quay biến tam giác đều thành chính nó là các phép quay 120o, 240o hoặc 360o tâm O cùng chiều hay ngược chiều kim đồng hồ.
b) Hình vuông. Các phép quay biến hình vuông thành chính nó là các phép quay 90o, 180o, 270o, 360o tâm I cùng chiều hay ngược chiều kim đồng hồ.
c) Ngũ giác đều. Các phép quay biến ngũ giác đều thành chính nó là các phép quay 72o, 144o, 216o, 288o, 360o tâm A cùng chiều hay ngược chiều kim đồng hồ.
d) Lục giác đều. Các phép quay biến lục giác đều thành chính nó là các phép quay 60o, 120o, 180o, 240o, 300o, 360o tâm B cùng chiều hay ngược chiều kim đồng hồ.
e) Bát giác đều. Các phép quay biến bát giác đều thành chính nó là các phép quay 45o, 90o, 135o, 180o, 225o, 270o, 315o, 360o tâm C cùng chiều hay ngược chiều kim đồng hồ.
(Trả lời bởi Nguyễn Quốc Đạt)
Đường viền ngoài của chiếc đồng hồ trong Hình 13 được làm theo hình đa giác đều nào? Tìm phép quay biến đa giác này thành chính nó.

Thảo luận (1)Hướng dẫn giảiĐường viền ngoài của chiếc đồng hồ trong Hình 13 được làm theo hình bát giác đều.
8 đỉnh của đa giác được chia thành 8 phần bằng nhau, mỗi cung có số đo 45o. Do đó, các phép quay biến bát giác đều thành chính nó là 45o, 90o, 135o, 180o, 225o, 270o, 315o, 360o theo chiều hoặc ngược chiều kim đồng hồ.
(Trả lời bởi Nguyễn Quốc Đạt)
Tìm các hình phẳng có tính đều:
a) Trong tự nhiên;
b) Trong sản xuất, thiết kế, mĩ thuật.
Thảo luận (1)Hướng dẫn giảia) Trong tự nhiên: mật ong, hoa tuyết,...
b) Trong sản xuất, thiết kế, mĩ thuật: trang trí nội thất, gạch,...
(Trả lời bởi Nguyễn Quốc Đạt)
Vòng trong của mái giếng trời hình hoa sen của nhà ga Bến Thành (Thành phố Hồ Chí Minh) có dạng đa giác đều 12 cạnh (Hình 14).
Hãy chỉ ra các phép quay biến đa giác đều thành chính nó.

Thảo luận (1)Hướng dẫn giải12 đỉnh của đa giác chia đường tròn thành 12 phần bằng nhau. Số đo mỗi cung là 30o. Do đó, các phép quay biến đa giác này thành chính nó là các phép quay 30o, 60o, 90o, 120o, 150o, 180o, 210o, 240o, 270o, 300o, 330o hoặc 360o theo chiều kim đồng hồ hay ngược chiều kim đồng hồ.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho đường tròn (O; R).
a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên (O; R).
b) Tính các cạnh của các hình vừa vẽ theo R.
Thảo luận (1)Hướng dẫn giảia)
b) Tam giác đều nội tiếp đường tròn nên ta có:
R = \(\frac{{a\sqrt 3 }}{3}\) (a là độ dài cạnh tam giác đều)
Suy ra a = \(\frac{{3R}}{{\sqrt 3 }} = R\sqrt 3 \)
Hình vuông nội tiếp đường tròn nên ta có:
\(R = \frac{d}{2}\) (d là đường chéo của hình vuông)
Suy ra d = 2R. Gọi x là độ dài cạnh hình vuông hay \(\sqrt {{x^2} + {x^2}} = 2R\) suy ra \(x\sqrt 2 = 2R\)
Hay x = \(\frac{{2R}}{{\sqrt 2 }} = R\sqrt 2 \)
Trong lục giác đều có khoảng cách từ tâm đến các đỉnh là bằng nhau (= R); các góc ở tâm đều bằng 60o nên lục giác đều gồm 6 tam giác đều.
Suy ra độ dài cạnh của lục giác đều là R.
(Trả lời bởi Nguyễn Quốc Đạt)
Em hãy tìm một số hình phẳng đều trong thực tế.
Thảo luận (1)Hướng dẫn giảiHình phẳng đều trong thực tế: rubik, bàn cờ,...
(Trả lời bởi Nguyễn Quốc Đạt)