Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(−3;−1; 0). Tìm tọa độ:
a) Các điểm M', N', P' lần lượt là trung điểm của các cạnh NP, MP, MN;
b) Trọng tâm G của tam giác M'N'P'.
Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(−3;−1; 0). Tìm tọa độ:
a) Các điểm M', N', P' lần lượt là trung điểm của các cạnh NP, MP, MN;
b) Trọng tâm G của tam giác M'N'P'.
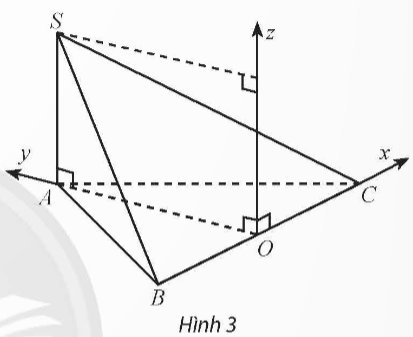
Cho hình chóp S.ABC có SA \(\perp\) (ABC), SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ tọa độ như Hình 3, hãy tìm tọa độ:
a) Các điểm A, S, B, C.
b) Trung điểm M của SB và trung điểm N của SC.
c) Trọng tâm G của tam giác SBC.
Thảo luận (1)Hướng dẫn giảia) \(OA = \sqrt {A{B^2} - O{B^2}} = \sqrt {{a^2} - {{(\frac{a}{2})}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(\overrightarrow {OA} = \frac{{a\sqrt 3 }}{2}\overrightarrow j = (0;\frac{{a\sqrt 3 }}{2};0) \Rightarrow A(0;\frac{{a\sqrt 3 }}{2};0)\)
\(\overrightarrow {OB} = - \frac{a}{2}\overrightarrow i = ( - \frac{a}{2};0;0) \Rightarrow B( - \frac{a}{2};0;0)\)
\(\overrightarrow {OC} = \frac{a}{2}\overrightarrow i = (\frac{a}{2};0;0) \Rightarrow C(\frac{a}{2};0;0)\)
\(\overrightarrow {OS} = \frac{{a\sqrt 3 }}{2}\overrightarrow j + a\overrightarrow k = (0;\frac{{a\sqrt 3 }}{2};a) \Rightarrow S(0;\frac{{a\sqrt 3 }}{2};a)\)
b) \(M(\frac{{0 - \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(M( - \frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
\(N(\frac{{0 + \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(N(\frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
c) \(G(\frac{{0 + \frac{a}{2} - \frac{a}{2}}}{3};\frac{{\frac{{a\sqrt 3 }}{2}}}{3};\frac{a}{3})\) hay \(G(0;\frac{{a\sqrt 3 }}{6};\frac{a}{3})\)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho tam giác MNP có M(0; 1; 2), N(5; 9; 3), P(7; 8; 2).
a) Tìm tọa độ điểm K là chân đường cao kẻ từ M của tam giác MNP.
b) Tìm độ dài các cạnh MN và MP.
c) Tính góc M.
Thảo luận (1)Hướng dẫn giảia) Ta có: \(\overrightarrow {NP} = (2; - 1; - 1)\)
Gọi K(x;y;z) là chân đường cao kẻ từ M của tam giác MNP
=> \(\overrightarrow {NK} = (x - 5;y - 9;z - 3)\)
\(\overrightarrow {NK} \) cùng phương với \(\overrightarrow {NP} \) nên \(x - 5 = 2t;y - 9 = - t;z - 3 = - t\) => \(K(2t + 2; - t + 9; - t + 3)\)
Ta có: \(\overrightarrow {MK} = (2t + 2; - t + 8; - t + 1)\)
\(\overrightarrow {MK} \bot \overrightarrow {NP} \Leftrightarrow \overrightarrow {MK} .\overrightarrow {NP} = 0 \Leftrightarrow (2t + 2).2 - ( - t + 8) - ( - t + 1) = 0 \Leftrightarrow t = \frac{5}{6}\)
Vậy \(K(\frac{{11}}{3};\frac{{49}}{6};\frac{{13}}{6})\)
b) Ta có: \(\overrightarrow {MN} = (5;8;1) \Rightarrow MN = \sqrt {{5^2} + {8^2} + {1^2}} = 3\sqrt {10} \)
\(\overrightarrow {MP} = (7;7;0) \Rightarrow MP = \sqrt {{7^2} + {7^2}} = 7\sqrt 2 \)
c) \(\cos M = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{|\overrightarrow {MN} |.|\overrightarrow {MP} |}} = \frac{{5.7 + 8.7}}{{3\sqrt {10} .7\sqrt 2 }} = \frac{{13\sqrt 5 }}{{30}}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một đội gồm ba drone giao hàng A, B, C đang có tọa độ là A(1; 1; 1), B(5; 7; 9), C(9; 11; 4). Tính:
a) Các khoảng cách giữa mỗi cặp drone giao hàng.
b) Góc \(\widehat{BAC}\).
Thảo luận (1)Hướng dẫn giảia) \(\overrightarrow {AB} = (4;6;8) \Rightarrow AB = \sqrt {{4^2} + {6^2} + {8^2}} = 2\sqrt {29} \)
\(\overrightarrow {AC} = (8;10;3) \Rightarrow \sqrt {{8^2} + {{10}^2} + {3^2}} = \sqrt {173} \)
\(\overrightarrow {BC} = (4;4; - 5) \Rightarrow \sqrt {{4^2} + {4^2} + {{( - 5)}^2}} = \sqrt {57} \)
c) \(\cos \widehat {BAC} = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{|\overrightarrow {AB} |.|\overrightarrow {AC} |}} = \frac{{4.8 + 6.10 + 8.3}}{{2\sqrt {29} .\sqrt {173} }} \approx 0,82 \Rightarrow \widehat {BAC} = 35,03^\circ \)
(Trả lời bởi Nguyễn Quốc Đạt)
Tính:
a) \(\overrightarrow{a}.\overrightarrow{b}\) với \(\overrightarrow{a}=\left(5;2;-4\right)\), \(\overrightarrow{b}=\left(4;-2;2\right)\).
b) \(\overrightarrow{c}.\overrightarrow{d}\) với \(\overrightarrow{c}=\left(2;-3;4\right)\), \(\overrightarrow{d}=\left(6;5;-3\right)\).
Thảo luận (1)Hướng dẫn giảia) \(\overrightarrow a .\overrightarrow b = 5.4 + 2.( - 2) - 4.2 = 8\)
b) \(\overrightarrow c .\overrightarrow d = 2.6 - 3.5 + 4.( - 3) = - 15\)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hai vectơ \(\overrightarrow{a}=\left(0;1;3\right)\) và \(\overrightarrow{b}=\left(-2;3;1\right)\). Tìm tọa độ của vectơ \(2\overrightarrow{b}-\dfrac{3}{2}\overrightarrow{a}\).
Thảo luận (1)Hướng dẫn giải\(2\overrightarrow b - \frac{3}{2}\overrightarrow a = 2(-2;3;1) - \frac{3}{2}(0;1;3) = (-4;\frac{9}{2};-\frac{5}{2})\)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho ba điểm A(2; 1; −1), B(3; 2; 0) và C(2; −1; 3).
a) Chứng minh A, B, C là ba đỉnh của một tam giác. Tính chu vi tam giác ABC.
b) Tìm tọa độ trung điểm của các cạnh của tam giác ABC.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
Thảo luận (1)Hướng dẫn giảia) Ta có \(\overrightarrow{AB} = (1; 1; 1)\), \(\overrightarrow{AC} = (0; -2; 4)\), \(\overrightarrow{BC} = (-1; -3; 3)\).
Vì \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) không cùng phương nên A, B, C không thẳng hàng.
Do đó A, B, C là ba đỉnh của một tam giác.
Ta có chu vi tam giác ABC là:
AB + AC + BC
= \(\sqrt{1^2 + 1^2 + 1^2} + \sqrt{0^2 + (-2)^2 + 4^2} + \sqrt{(-1)^2 + (-3)^2 + 3^2}\)
= \(\sqrt{3} + 2\sqrt{5} + \sqrt{19}\)
b) Gọi A’, B’, C’ lần lượt là trung điểm của AB, BC, AC
Ta có: \(A'(\frac{{2 + 3}}{2};\frac{{1 + 2}}{2};\frac{{ - 1}}{2})\) hay \(A'(\frac{5}{2};\frac{3}{2}; - \frac{1}{2})\)
\(B'(\frac{{3 + 2}}{2};\frac{{2 - 1 }}{2};\frac{3}{2})\) hay \(B'(\frac{5}{2};\frac{1}{2}; \frac{3}{2})\)
\(C'(\frac{{2 + 2}}{2};\frac{{1 - 1}}{2};\frac{{ - 1 + 3}}{2})\) hay \(C'(2;0;1)\)
c) \(G(\frac{{2 + 3 + 2}}{3};\frac{{1 + 2 - 1}}{3};\frac{{ - 1 + 3}}{3})\) hay \(G(\frac{7}{3};\frac{2}{3};\frac{2}{3})\)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho điểm M(1; 2; 3). Hãy tìm tọa độ của các điểm:
a) M1, M2, M3 lần lượt là hình chiếu vuông góc của M trên các mặt phẳng (Oxy), (Oyz), (Oxz).
b) Gọi M', M", M"' lần lượt là các điểm thỏa mãn:
• O là trung điểm của MM'
• MM" vuông góc với mặt phẳng (Oxy) tại điểm H sao cho H là trung điểm của MM".
• MM"' vuông góc và cắt trục Oy tại điểm K sao cho K là trung điểm của MM"'.
Thảo luận (1)Hướng dẫn giảia) \({M_1}(1;2;0),{M_2}(0;2;3),{M_3}(1;0;3)\).
b)
+) Vì O là trung điểm của MM’ nên
\(\left\{ {\begin{array}{*{20}{c}}{{x_{M'}} = 2{x_O} - {x_M}}\\{{y_{M'}} = 2{y_O} - {y_M}}\\{{z_{M'}} = 2{z_O} - {z_M}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_{M'}} = 2.0 - 1}\\{{y_{M'}} = 2.0 - 2}\\{{z_{M'}} = 2.0 - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_{M'}} = - 1}\\{{y_{M'}} = - 2}\\{{z_{M'}} = - 3}\end{array}} \right.\)
Vậy M’(-1;-2;-3).
+) Vì M’’ đối xứng với M qua mặt phẳng Oxy nên \({M_1}\) là trung điểm của MM’’. Khi đó
\(\left\{ {\begin{array}{*{20}{c}}{{x_{M''}} = 2{x_{{M_1}}} - {x_M}}\\{{y_{M''}} = 2{y_{{M_1}}} - {y_M}}\\{{z_{M''}} = 2{z_{{M_1}}} - {z_M}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_{M''}} = 2.1 - 1}\\{{y_{M''}} = 2.2 - 2}\\{{z_{M''}} = 2.0 - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_{M''}} = 1}\\{{y_{M''}} = 2}\\{{z_{M''}} = - 3}\end{array}} \right.\)
Vậy M’’(1;2;-3).
+) K là hình chiếu của M trên Oy nên K(0;2;0).
Vì K là trung điểm của MM’’’ nên
\(\left\{ {\begin{array}{*{20}{c}}{{x_{M'''}} = 2{x_K} - {x_M}}\\{{y_{M'''}} = 2{y_K} - {y_M}}\\{{z_{M'''}} = 2{z_K} - {z_M}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_{M''}} = 2.0 - 1}\\{{y_{M''}} = 2.2 - 2}\\{{z_{M''}} = 2.0 - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_{M''}} = - 1}\\{{y_{M''}} = 2}\\{{z_{M''}} = - 3}\end{array}} \right.\)
Vậy M’’’(-1;2;-3).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho ba điểm A(3; 3; 3), B(1; 1; 2) và C(5; 3; 1).
a) Tìm điểm M trên trục Oy cách đều hai điểm B, C.
b) Tìm điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C.
Thảo luận (1)Hướng dẫn giảia) \(M(0;{y_M};0)\)
M cách đều B và C => MB = MC
Ta có:
\(\overrightarrow {MC} = (5;3 - {y_M};1) = > MC = \sqrt {26 + {{(3 - {y_M})}^2}} \)
MB = MC \( \Leftrightarrow \sqrt {5 + {{(1 - {y_M})}^2}} = \sqrt {26 + {{(3 - {y_M})}^2}} \Leftrightarrow {y_M} = \frac{{29}}{4}\)
=> \(M(0;\frac{{29}}{4};0)\)
b) \(N({x_N};{y_N};0)\)
Ta có: \(\overrightarrow {NA} = (3 - {x_N};3 - {y_n};3) \Rightarrow NA = \sqrt {{{(3 - {x_N})}^2} + {{(3 - {y_n})}^2} + 9} \)
\(\overrightarrow {NB} = (1 - {x_N};1 - {y_n};2) \Rightarrow NB = \sqrt {{{(1 - {x_N})}^2} + {{(1 - {y_n})}^2} + 4} \)
\(\overrightarrow {NC} = (5 - {x_N};3 - {y_n};1) \Rightarrow NC = \sqrt {{{(5 - {x_N})}^2} + {{(3 - {y_n})}^2} + 1} \)
N cách đều ba điểm A, B, C nên NA = NB = NC
\(\left\{ \begin{array}{l}\sqrt {{{(3 - {x_N})}^2} + {{(3 - {y_n})}^2} + 9} = \sqrt {{{(1 - {x_N})}^2} + {{(1 - {y_n})}^2} + 4} \\\sqrt {{{(3 - {x_N})}^2} + {{(3 - {y_n})}^2} + 9} = \sqrt {{{(5 - {x_N})}^2} + {{(3 - {y_n})}^2} + 1} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = - 3\\{y_N} = \frac{{33}}{4}\end{array} \right.\)
Vậy \(N( - 3;\frac{{33}}{4};0)\)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho các điểm A(−1; −1; 0), B(0; 3; −1), C(−1; 14; 0), D(−3; 6; 2). Chứng minh rằng ABCD là hình thang.
Thảo luận (1)Hướng dẫn giảiTa có: \(\overrightarrow {AB} = (1;4; - 1)\)
\(\overrightarrow {CD} = ( - 2; - 8;2)\)
=> \( - 2\overrightarrow {AB} = \overrightarrow {CD} \) => \(\overrightarrow {AB} //\overrightarrow {CD} \) => ABCD là hình thang
(Trả lời bởi Nguyễn Quốc Đạt)