Khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia. Hãy thảo luận để làm rõ nhận xét này.
Bài 26. Khoảng cách
Giải mục 3 trang 57, 58 (SGK Kết nối tri thức và cuộc sống)
Thảo luận (1)
Bài 7.22 trang 59 (SGK Kết nối tri thức và cuộc sống)
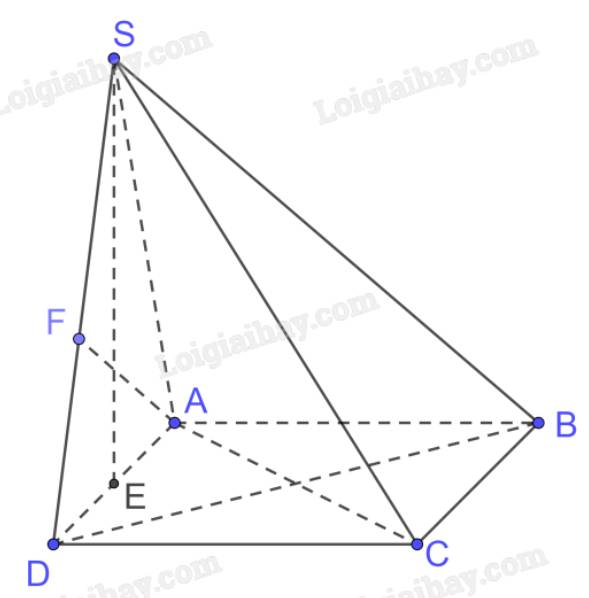
Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) ⊥ (ABCD).
a) Tính chiều cao của hình chóp.
b) Tính khoảng cách giữa BC và (SAD).
c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD.
Thảo luận (1)Hướng dẫn giải
a) Gọi E là trung điểm của AD
\(\left( {SAD} \right) \bot \left( {ABCD} \right),\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\)
Mà tam giác SAD đều
\( \Rightarrow \) \(SE \bot \left( {ABCD} \right)\)
Xét tam giác SDE vuông tại E có
\(SE = \sqrt {S{D^2} - D{E^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
b) Ta có \(AB \bot AD,AB \bot SE\left( {SE \bot \left( {ABCD} \right)} \right) \Rightarrow AB \bot \left( {SAD} \right)\)
Vì BC // AD (ABCD là hình vuông), \(AD \subset \left( {SAD} \right)\) nên BC // (SAD)
\( \Rightarrow \) d(BC, (SAD)) = d(B, (SAD)) = AB = a
c) Trong (SAD) kẻ \(AF \bot SD\)
Có \(AB \bot \left( {SAD} \right),AF \subset \left( {SAD} \right) \Rightarrow AB \bot AF\)
\( \Rightarrow \) d(AB, SD) = AF
Vì tam giác SAD đều nên \(AF = SE = \frac{{a\sqrt 3 }}{2}\)
Vậy \(d\left( {AB,{\rm{ }}SD} \right) = \frac{{a\sqrt 3 }}{2}\)
(Trả lời bởi Quoc Tran Anh Le)
Bài 7.23 trang 59 (SGK Kết nối tri thức và cuộc sống)
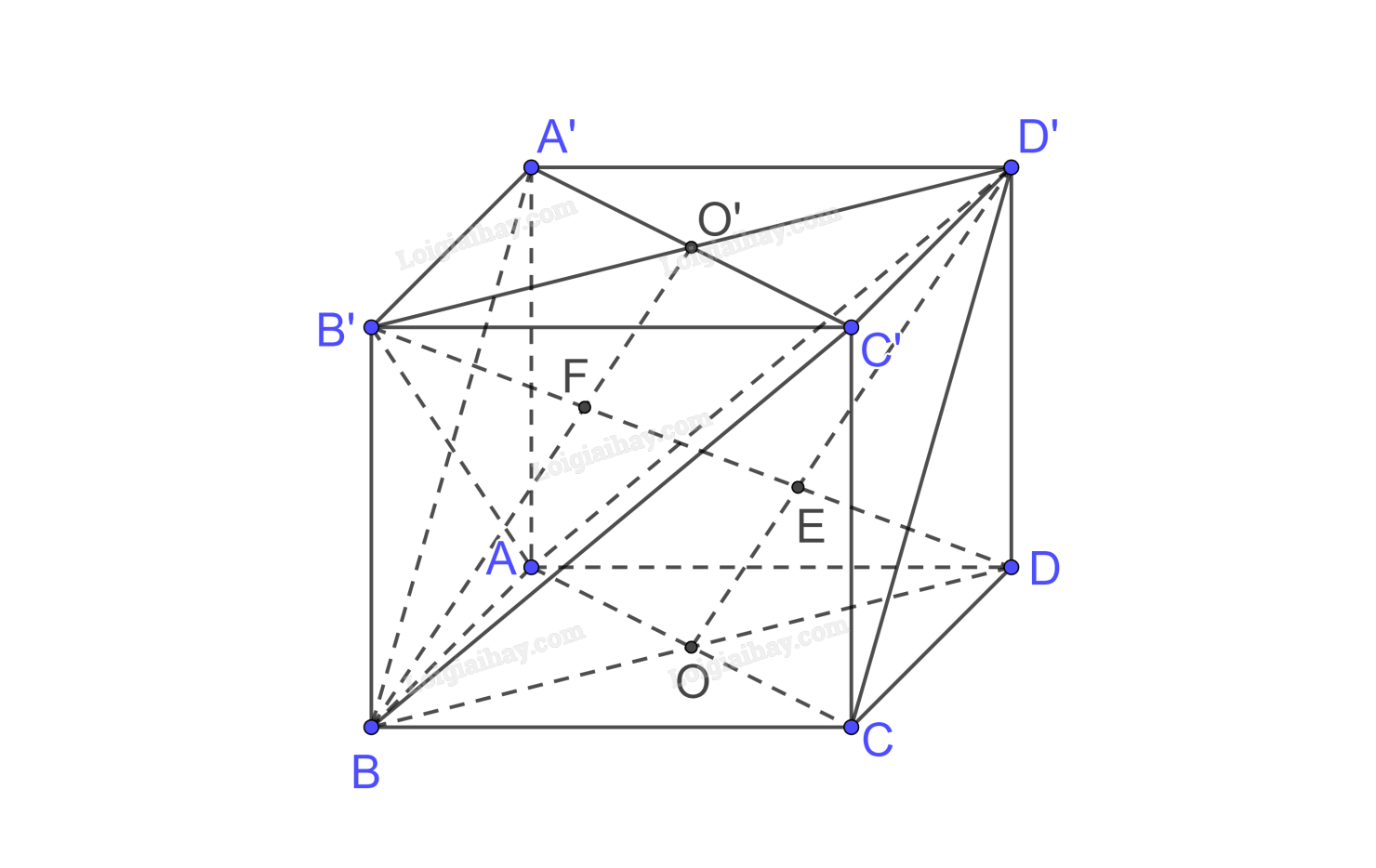
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, BC = c.
a) Tính khoảng cách giữa CC' và (BB'D'D).
b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.
Thảo luận (1)Hướng dẫn giải
a) Trong (ABCD) kẻ \(CE \bot BD\)
Mà \(CE \bot BB'\left( {BB' \bot \left( {ABCD} \right)} \right) \Rightarrow CE \bot \left( {BB'D'D} \right)\)
Ta có CC’ // BB’ \( \Rightarrow \) CC’ // (BB’D’D) \( \Rightarrow \) d(CC’, (BB’D’D)) = d(C, (BB’D’D)) = CE
Xét tam giác BCD vuông tại C có
\(\frac{1}{{C{E^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{C{D^2}}} = \frac{1}{{{c^2}}} + \frac{1}{{{b^2}}} = \frac{{{b^2} + {c^2}}}{{{c^2}{b^2}}} \Rightarrow CE = \frac{{bc}}{{\sqrt {{b^2} + {c^2}} }}\)
b) \(AC \subset \left( {ABCD} \right),B'D' \subset \left( {A'B'C'D'} \right),\left( {ABCD} \right)//\left( {A'B'C'D'} \right)\)
\( \Rightarrow d\left( {AC,B'D'} \right) = d\left( {\left( {ABCD} \right),\left( {A'B'C'D'} \right)} \right) = BB' = a\)
(Trả lời bởi Quoc Tran Anh Le)
Bài 7.24 trang 59 (SGK Kết nối tri thức và cuộc sống)
Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) MN là đường vuông góc chung của AB và CD.
b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.
Thảo luận (1)Hướng dẫn giải
Bài 7.25 trang 59 (SGK Kết nối tri thức và cuộc sống)
Cho hình lập phương ABCD.A'B'C'D' có cạnh a.
a) Chứng minh rằng hai mặt phẳng (D'AC) và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó.
b) Xác định các giao điểm E, F của DB' với (D'AC),(BC'A'). Tính d((D'AC), (BC'A')).
Thảo luận (1)Hướng dẫn giải
a) AC // A’C’, D’C // A’B \( \Rightarrow \) (D'AC) // (BC'A')
Ta có \(AC \bot BD,AC \bot BB' \Rightarrow AC \bot \left( {BDB'} \right);B'D \subset \left( {BDB'} \right) \Rightarrow AC \bot B'D\)
Mà AC // A’C’ \( \Rightarrow \) \(B'D \bot A'C'\)
Ta có \(AB' \bot A'B,AD \bot A'B \Rightarrow A'B \bot \left( {AB'D} \right);B'D \subset \left( {AB'D} \right) \Rightarrow A'B \bot B'D\)
Mà A’B // D’C \( \Rightarrow \) \(B'D \bot D'C\)
Ta có \(B'D \bot AC,B'D \bot D'C \Rightarrow B'D \bot \left( {D'AC} \right)\)
\(B'D \bot A'C',B'D \bot A'B \Rightarrow B'D \bot \left( {BA'C'} \right)\)
b) Gọi \(AC \cap BD = \left\{ O \right\},A'C' \cap B'D' = \left\{ {O'} \right\}\)
Trong (BB’D’D) nối \(D'O \cap B'D = \left\{ E \right\},BO' \cap B'D = \left\{ F \right\}\)
Vì (D'AC) // (BC'A') nên d((D'AC), (BC'A')) = d(E, (BC'A')) = EF do \(B'D \bot \left( {BA'C'} \right)\)
\(\left. \begin{array}{l}B'D \bot BO'\left( {B'D \bot \left( {BA'C'} \right)} \right)\\B'D \bot OD'\left( {B'D \bot \left( {D'AC} \right)} \right)\end{array} \right\} \Rightarrow BO'//OD'\)
Áp dụng định lí Talet có \(\frac{{DE}}{{EF}} = \frac{{DO}}{{BO}} = 1 \Rightarrow DE = EF\) và \(\frac{{B'F}}{{EF}} = \frac{{B'O'}}{{O'D'}} = 1 \Rightarrow B'F = EF\)
\( \Rightarrow EF = \frac{{B'D}}{3}\)
Xét tam giác ABD vuông tại A có \(BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
Xét tam giác BB’D vuông tại B có \(B'D = \sqrt {B{{B'}^2} + B{D^2}} = \sqrt {{a^2} + {{\left( {a\sqrt 2 } \right)}^2}} = a\sqrt 3 \)
\( \Rightarrow EF = \frac{{a\sqrt 3 }}{3}\)
Vậy \(d\left( {\left( {D'AC} \right),{\rm{ }}\left( {BC'A'} \right)} \right) = \frac{{a\sqrt 3 }}{3}\)
(Trả lời bởi Quoc Tran Anh Le)
Bài 7.26 trang 59 (SGK Kết nối tri thức và cuộc sống)
Giá đỡ ba chân ở Hình 7.90 đang được mở sao cho ba gốc chân cách đều nhau một khoảng cách bằng 110 cm. Tính chiều cao của giá đỡ, biết các chân của giá đỡ dài 129 cm.
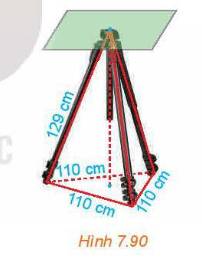
Thảo luận (1)Hướng dẫn giải`h` của đáy `=110 . \sqrt{3}/2 = 55\sqrt{3} (cm)`
`d` từ gốc `->`tâm `=2/3 . 55\sqrt{3} = (110\sqrt{3})/3 (cm)`
`h` giá đỡ `=\sqrt{129^{2} - ((110\sqrt{3})/3)^{2} } = \sqrt{37823/3} ~~112,28(cm)`
(Trả lời bởi Đức Anh Phùng)
Bài 7.27 trang 59 (SGK Kết nối tri thức và cuộc sống)
Một bể nước có đáy thuộc mặt phẳng nằm ngang. Trong trường hợp này, độ sâu của bể là khoảng cách giữa mặt nước và đáy bể. Giải thích vì sao để đo độ sâu của bể, ta có thể thả quả dọi chạm đáy bể và đo chiều dài của đoạn dây dọi năm trong bề nước.
Thảo luận (1)Hướng dẫn giảiKhi bể nước có đáy thuộc mặt phẳng nằm ngang, thì mặt nước nằm trong mặt phẳng song song với đáy. Vì vậy, để đo độ sâu của bể, ta có thể đo khoảng cách từ mặt nước đến đáy bể.
Khi thả quả dọi vào bể nước, nó sẽ chìm dưới mặt nước và chạm đến đáy bể. Khi kéo quả dọi lên, ta sẽ thấy một đoạn dây dọi nằm trong bể nước và một đoạn dây dọi ở ngoài bể nước. Đoạn dây dọi nằm trong bể nước có độ dài bằng khoảng cách từ mặt nước đến chỗ quả dọi chạm đáy bể. Do đó, để đo độ sâu của bể, ta chỉ cần đo độ dài của đoạn dây dọi nằm trong bể nước.
Công thức để tính độ sâu của bể nước sẽ là:
Độ sâu bể = chiều dài của đoạn dây dọi nằm trong bể nước
(Trả lời bởi Quoc Tran Anh Le)