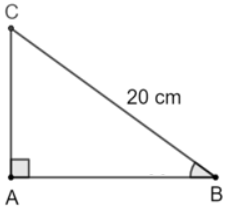
Cho tam giác ABC vuông tại A (Hình 1).
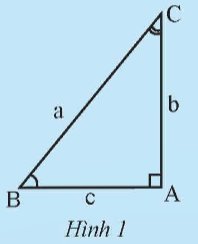
a) Hãy tính sin B theo b và a, cos B theo c và a. Sử dụng các kết quả tính được để giải thích tại sao ta lại có các đẳng thức: b = a.sin B; c = a.cos B
b) Hãy tính tan B theo b và c, cot B theo c và b. Sử dụng các kết quả tính được ở trên để giải thích tại sao ta lại có các đẳng thức: b = c.tan B; c = b.cot B.