Bài 2. Bất phương trình bậc nhất một ẩn

Hướng dẫn giải

a. Thay \(x =  - 3\), ta có: \({\left( { - 3} \right)^2} - 3.\left( { - 3} \right) + 2 > 0\) là khẳng định đúng.

Vậy \(x =  - 3\) là nghiệm của bất phương trình \({x^2} - 3x + 2 > 0\).

Thay \(x = 1,5\), ta có: \(1,{5^2} - 3.1,5 + 2 > 0\) là khẳng định sai.

Vậy \(x = 1,5\) không là nghiệm của bất phương trình \({x^2} - 3x + 2 > 0\).

b. Thay \(x = \frac{2}{5}\), ta có: \(2 - 2.\frac{2}{5} < 3.\frac{2}{5} + 1\) là khẳng định đúng.

Vậy \(x = \frac{2}{5}\)  là nghiệm của bất phương trình \(2 - 2x < 3x + 1\).

Thay \(x = \frac{1}{5}\), ta có: \(2 - 2.\frac{1}{5} < 3.\frac{1}{5} + 1\) là khẳng định sai.

Vậy \(x = \frac{1}{5}\) không là nghiệm của bất phương trình \(2 - 2x < 3x + 1\). 

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

a.

\(\begin{array}{l}2x + 6 > 1\\2x >  - 5\\x > \frac{{ - 5}}{2}\end{array}\)

Vậy nghiệm của bất phương trình là \(x > \frac{{ - 5}}{2}\).

b.

\(\begin{array}{l}0,6x + 2 > 6x + 9\\0,6x + 2 - 6x - 9 > 0\\ - 5,4x - 7 > 0\\ - 5,4x > 7\\x <  - \frac{{35}}{{27}}\end{array}\)

Vậy nghiệm của bất phương trình là \(x <  - \frac{{35}}{{27}}\).

c.

\(\begin{array}{l}1,7x + 4 \ge 2 + 1,5x\\1,7x + 4 - 2 - 1,5x \ge 0\\0,2x + 2 \ge 0\\0,2x \ge  - 2\\x \ge  - 10\end{array}\)

Vậy nghiệm của bất phương trình là \(x \ge  - 10\).

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

a.

\(\begin{array}{l}\frac{{8 - 3x}}{2} - x < 5\\\frac{{8 - 3x}}{2} - \frac{{2x}}{2} < \frac{5}{2}\\\frac{{8 - 3x - 2x}}{2} - \frac{5}{2} < 0\\\frac{{8 - 3x - 2x - 5}}{2} < 0\\\frac{{ - 5x + 3}}{2} < 0\\ - 5x + 3 < 0\\ - 5x <  - 3\\x > \frac{3}{5}\end{array}\)

Vậy nghiệm của bất phương trình là \(x > \frac{3}{5}\).

b.

\(\begin{array}{l}3 - 2x - \frac{{6 + 4x}}{3} > 0\\\frac{9}{3} - \frac{{6x}}{3} - \frac{{6 + 3x}}{3} > 0\\\frac{{9 - 6x - 6 - 3x}}{3} > 0\end{array}\)

\(\begin{array}{l}\frac{{ - 9x + 3}}{3} > 0\\ - 9x >  - 3\\x < \frac{1}{3}\end{array}\)

Vậy nghiệm của bất phương trình là \(x < \frac{1}{3}\).

c.

\(\begin{array}{l}0,7x + \frac{{2x - 4}}{3} - \frac{x}{6} > 1\\\frac{{4,2x}}{6} + \frac{{2.\left( {2x - 4} \right)}}{6} - \frac{x}{6} > \frac{1}{6}\\4,2x + 4x - 8 - x - 1 > 0\\7,2x - 9 > 0\\7,2x > 9\\x > \frac{5}{4}\end{array}\)

Vậy nghiệm của bất phương trình là \(x > \frac{5}{4}\).

(Trả lời bởi Hà Quang Minh)

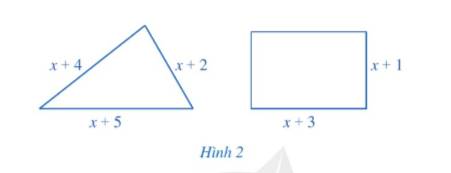
Hướng dẫn giải

+ Chu vi của hình tam giác là: \(x + 4 + x + 5 + x + 2 = 3x + 11\).

+ Chu vi của hình chữ nhật là: \(2.\left( {x + 3 + x + 1} \right) = 2\left( {2x + 4} \right) = 4x + 8\).

+ Để chu vi của hình tam giác lớn hơn chu vi của hình chữ nhật ta có bất phương trình:

\(\begin{array}{l}3x + 11 > 4x + 8\\3x + 11 - 4x - 8 > 0\\ - x + 3 > 0\\ - x >  - 3\\x < 3\end{array}\)

Mà \(x > 0\) nên ta có \(0 < x < 3\).

Vậy \(x \in \left\{ {1;2} \right\}\) thỏa mãn yêu cầu đề bài.

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Khối lượng xi măng xuất đi trong \(x\) ngày là: \(20x\) (tấn)

Khối lượng xi măng còn lại sau \(x\) ngày là: \(100 - 20x\) (tấn)

Để khối lượng xi măng còn lại trong kho ít nhất là 10 tấn thì

\(100 - 20x \ge 10\).

Giải bất phương trình trên, ta có:

\(\begin{array}{l}100 - 20x \ge 10\\ - 20x \ge 10 - 100\\ - 20x \ge  - 90\\x \le 4,5\end{array}\)

Vậy kho phải xuất 4 ngày để số xi măng còn lại trong kho ít nhất là 10 tấn.

(Trả lời bởi Hà Quang Minh)