Trong không gian Oxyz, cho mặt phẳng (α): x + 2 = 0.
a) Điểm A(−2; 1; 0) có thuộc (α) hay không?
b) Hãy chỉ ra một vectơ pháp tuyến của (α).
Bài 14. Phương trình mặt phẳng
Luyện tập 5 (SGK Kết nối tri thức với cuộc sống - Trang 32)
Thảo luận (1)
Hoạt động 5 (SGK Kết nối tri thức với cuộc sống - Trang 33)
Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M0(x0; y0; z0) và có vectơ pháp tuyến \(\overrightarrow{n}=\left(A;B;C\right)\).
Dựa vào Hoạt động 4, hãy nêu phương trình của (α).
Thảo luận (1)Hướng dẫn giảiGọi điểm M(x; y; z) thuộc \(\left( \alpha \right)\). Khi đó, hai vectơ \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \) vuông góc với nhau.
Ta có: \(\overrightarrow {{M_o}M} \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\)
Suy ra phương trình của \(\left( \alpha \right)\) là: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)
\( \Leftrightarrow Ax + By + Cz - A{x_0} - B{y_0} - C{z_0} = 0\)
Vậy phương trình của \(\left( \alpha \right)\) là: \(Ax + By + Cz - A{x_0} - B{y_0} - C{z_0} = 0\)
(Trả lời bởi datcoder)
Luyện tập 6 (SGK Kết nối tri thức với cuộc sống - Trang 33)
Trong không gian Oxyz, viết phương trình mặt phẳng (α) đi qua điểm M(1; 2; −4) và vuông góc với trục Oz.
Thảo luận (1)Hướng dẫn giảiVì mặt phẳng \(\left( \alpha \right)\) vuông góc với trục Oz nên mặt phẳng \(\left( \alpha \right)\) nhận \(\overrightarrow n \left( {0;0;1} \right)\) làm một vectơ pháp tuyến. Mà mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( {1;2; - 4} \right)\) nên phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\) là: \(0\left( {x - 1} \right) + 0\left( {y - 2} \right) + 1.\left( {z + 4} \right) = 0 \Leftrightarrow z + 4 = 0\)
(Trả lời bởi datcoder)
Hoạt động 6 (SGK Kết nối tri thức với cuộc sống - Trang 33)
Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M(x0; y0; z0) và biết cặp vectơ chỉ phương \(\overrightarrow{u}\) = (a; b; c), \(\overrightarrow{v}\) = (a′; b′; c′).
a) Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (α).
b) Viết phương trình mặt phẳng (α).
Thảo luận (1)Hướng dẫn giảia) Vì \(\overrightarrow u ,\overrightarrow v \) là các vectơ chỉ phương của mặt phẳng \(\left( \alpha \right)\). Do đó, \(\overrightarrow u ,\overrightarrow v \) cùng vuông góc với vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
Một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) là: \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\).
b) Vì mặt phẳng \(\left( \alpha \right)\) có một vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\) và đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) nên phương trình mặt phẳng \(\left( \alpha \right)\) là:
\(\left( {bc' - b'c} \right)\left( {x - {x_0}} \right) + \left( {ca' - c'a} \right)\left( {y - {y_0}} \right) + \left( {ab' - a'b} \right)\left( {z - {z_0}} \right) = 0\)
(Trả lời bởi datcoder)
Luyện tập 7 (SGK Kết nối tri thức với cuộc sống - Trang 34)
Trong không gian Oxyz, cho các điểm A(1; −2; −1), B(4; 1; 2), C(2; 3; 1). Viết phương trình mặt phẳng (α) đi qua điểm A(1; −2; −1) đồng thời song song với trục Oy và đường thẳng BC.
Thảo luận (1)Hướng dẫn giảiTrục Oy có một vectơ chỉ phương là: \(\overrightarrow j = \left( {0;1;0} \right)\).
Đường thẳng BC có một vectơ chỉ phương là: \(\overrightarrow {BC} \left( { - 2;2; - 1} \right)\).
Vì mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {1; - 2; - 1} \right)\) đồng thời song song với trục Oy và đường thẳng BC nên mặt phẳng \(\left( \alpha \right)\) nhận \(\overrightarrow n = \left[ {\overrightarrow {BC} ,\overrightarrow j } \right]\) làm một vectơ pháp tuyến.
\(\overrightarrow n = \left[ {\overrightarrow {BC} ,\overrightarrow j } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&{ - 2}\\0&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&2\\0&1\end{array}} \right|} \right) = \left( {1;0; - 2} \right)\)
Do đó, phương trình mặt phẳng \(\left( \alpha \right)\) là: \(1\left( {x - 1} \right) - 2\left( {z + 1} \right) = 0 \Leftrightarrow x - 2z - 3 = 0\)
(Trả lời bởi datcoder)
Hoạt động 7 (SGK Kết nối tri thức với cuộc sống - Trang 34)
Trong không gian Oxyz, cho ba điểm không thẳng hàng: A(1; 2; 3), B(−1; 3; 4), C(2; −1; 2).
a) Hãy chỉ ra một cặp vectơ chỉ phương của mặt phẳng (ABC).
b) Viết phương trình mặt phẳng (ABC).
Thảo luận (1)Hướng dẫn giảia) Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - 2;1;1} \right),\overrightarrow {AC} \left( {1, - 3; - 1} \right)\).
b) Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - 2;1;1} \right),\overrightarrow {AC} \left( {1, - 3; - 1} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
Ta có: \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&1\\{ - 3}&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&{ - 2}\\{ - 1}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&1\\1&{ - 3}\end{array}} \right|} \right) = \left( {2; - 1;5} \right)\)
Mặt phẳng (ABC) đi qua điểm \(A\left( {1;2;3} \right)\) có vectơ pháp tuyến \(\overrightarrow n = \left( {2; - 1;5} \right)\) nên phương trình mặt phẳng (ABC) là: \(2\left( {x - 1} \right) - \left( {y - 2} \right) + 5\left( {z - 3} \right) = 0 \Leftrightarrow 2x - y + 5z - 15 = 0\).
(Trả lời bởi datcoder)
Luyện tập 8 (SGK Kết nối tri thức với cuộc sống - Trang 35)
(H.5.8) Trong không gian Oxyz, cho mặt phẳng (α) không đi qua gốc tọa độ và cắt ba trục Ox, Oy, Oz tương ứng tại các điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) (a, b, c ≠ 0).
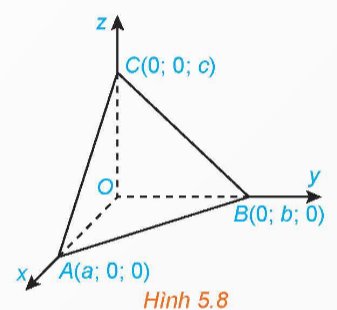
Chứng minh rằng mặt phẳng (α) có phương trình: \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\).
Thảo luận (1)Hướng dẫn giảiMặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - a;b;0} \right),\overrightarrow {AC} \left( { - a;0;c} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
Ta có: \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}b&0\\0&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - a}\\c&{ - a}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - a}&b\\{ - a}&0\end{array}} \right|} \right) = \left( {bc;ac;ab} \right)\)
Mặt phẳng (ABC) đi qua điểm A(a; 0; 0) và vectơ pháp tuyến \(\overrightarrow n = \left( {bc;ac;ab} \right)\) nên phương trình mặt phẳng (ABC) là:
\(bc\left( {x - a} \right) + acy + abz = 0 \Leftrightarrow bcx + acy + abz = bca \Leftrightarrow \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) (đpcm)
(Trả lời bởi datcoder)
Vận dụng 2 (SGK Kết nối tri thức với cuộc sống - Trang 35)
Trong tình huống mở đầu, hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra.a) Xác định tọa độ của vị trí M1, M2, M3 của vật tương ứng với các thời điểm t 0, t dfrac{pi}{2}, t π.b) Chứng minh rằng M1, M2, M3 không thẳng hàng và viết phương trình mặt phẳng (M1M2M3).c) Vị trí M(cost – sint; cost + sint; cost) có luôn thuộc mặt phẳng (M1M2M3) hay không?
Đọc tiếp
Trong tình huống mở đầu, hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra.
a) Xác định tọa độ của vị trí M1, M2, M3 của vật tương ứng với các thời điểm t = 0, t = \(\dfrac{\pi}{2}\), t = π.
b) Chứng minh rằng M1, M2, M3 không thẳng hàng và viết phương trình mặt phẳng (M1M2M3).
c) Vị trí M(cost – sint; cost + sint; cost) có luôn thuộc mặt phẳng (M1M2M3) hay không?
Thảo luận (1)Hướng dẫn giảia) Với \(t = 0\) ta có: \({M_1}\left( {1;1;1} \right)\)
Với \(t = \frac{\pi }{2}\) ta có: \({M_2}\left( { - 1;1;0} \right)\)
Với \(t = \pi \) ta có: \({M_3}\left( { - 1; - 1; - 1} \right)\)
b) Hai vectơ \(\overrightarrow {{M_1}{M_2}} \left( { - 2;0; - 1} \right),\overrightarrow {{M_1}{M_3}} \left( { - 2; - 2; - 2} \right)\) không cùng phương nên ba điểm \({M_1},{M_2},{M_3}\) không thẳng hàng.
c) Mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) có cặp vectơ chỉ phương \(\overrightarrow {{M_1}{M_2}} \left( { - 2;0; - 1} \right),\overrightarrow {{M_1}{M_3}} \left( { - 2; - 2; - 2} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {{M_1}{M_2}} ,\overrightarrow {{M_1}{M_3}} } \right]\).
Ta có: \(\overrightarrow n = \left[ {\overrightarrow {{M_1}{M_2}} ,\overrightarrow {{M_1}{M_3}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 1}\\{ - 2}&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&{ - 2}\\{ - 2}&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&0\\{ - 2}&{ - 2}\end{array}} \right|} \right) = \left( { - 2; - 2;4} \right)\)
Mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) có vectơ pháp tuyến \(\overrightarrow n \left( { - 2; - 2;4} \right)\) và đi qua điểm \({M_2}\left( { - 1;1;0} \right)\) nên phương trình mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) là:
\( - 2\left( {x + 1} \right) - 2\left( {y - 1} \right) + 4z = 0 \Leftrightarrow x + 1 + y - 1 - 2z = 0 \Leftrightarrow x + y - 2z = 0\) (1)
c) Với \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) thay vào (1) ta có:
$\cos t-\sin t+\cos t+\sin t-2\cos t=0\Leftrightarrow 0=0\left( L D\right)$
Vậy \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) thuộc mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\). Do đó, vật thể M luôn chuyển động trong một mặt phẳng cố định.
(Trả lời bởi datcoder)
Hoạt động 8 (SGK Kết nối tri thức với cuộc sống - Trang 35)
Trong không gian Oxyz, cho hai mặt phẳng: (α): Ax + By + Cz + D 0, (β): Ax + By + Cz + D 0, với hai vectơ pháp tuyến overrightarrow{n} (A; B; C), overrightarrow{n} (A′; B′; C′) tương ứng.a) Góc giữa hai mặt phẳng (α), (β) và góc giữa hai giá của overrightarrow{n} , overrightarrow{n} có mối quan hệ gì?b) Hai mặt phẳng (α) và (β) vuông góc với nhau khi và chỉ khi hai vectơ pháp tuyến tương ứngoverrightarrow{n}, overrightarrow{n} có mối quan hệ gì?
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng: (α): Ax + By + Cz + D = 0, (β): A'x + B'y + C'z + D' = 0, với hai vectơ pháp tuyến \(\overrightarrow{n}\)= (A; B; C), \(\overrightarrow{n'}\) = (A′; B′; C′) tương ứng.
a) Góc giữa hai mặt phẳng (α), (β) và góc giữa hai giá của \(\overrightarrow{n}\) , \(\overrightarrow{n'}\) có mối quan hệ gì?
b) Hai mặt phẳng (α) và (β) vuông góc với nhau khi và chỉ khi hai vectơ pháp tuyến tương ứng\(\overrightarrow{n}\), \(\overrightarrow{n'}\) có mối quan hệ gì?
Thảo luận (1)Hướng dẫn giảia) Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng bất kì tương ứng vuông góc với hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\).
Mà giá của \(\overrightarrow n \) vuông góc với mặt phẳng \(\left( \alpha \right)\), giá của \(\overrightarrow {n'} \) vuông góc với mặt phẳng \(\left( \beta \right)\).
Do đó, góc giữa hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) bằng góc giữa hai giá của \(\overrightarrow n ,\overrightarrow {n'} \).
b) Hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) vuông góc với nhau khi và chỉ khi góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) bằng \({90^o}\), do đó, hai vectơ pháp tuyến \(\overrightarrow n ,\overrightarrow {n'} \) vuông góc với nhau.
(Trả lời bởi datcoder)
Luyện tập 9 (SGK Kết nối tri thức với cuộc sống - Trang 36)
Trong không gian Oxyz, hai mặt phẳng sau đây có vuông góc với nhau hay không? (α): 3x + y – z + 1 = 0, (β): 9x + 3y – 3z + 3 = 0.
Thảo luận (1)Hướng dẫn giảiMặt phẳng \(\left( \alpha \right)\) có 1 vectơ pháp tuyến là \(\overrightarrow {{n_1}} \left( {3;1; - 1} \right)\), mặt phẳng \(\left( \beta \right)\) có 1 vectơ pháp tuyến là \(\overrightarrow {{n_2}} \left( {9;3; - 3} \right)\). Ta có: \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 3.9 + 1.3 + 3.1 = 33 \ne 0\) nên hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) không vuông góc với nhau.
(Trả lời bởi datcoder)