Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.
Bài 14. Hình thoi và hình vuông
Bài 3.31 (SGK Kết nối tri thức với cuộc sống - Trang 72)
Thảo luận (1)
Bài 3.32 (SGK Kết nối tri thức với cuộc sống - Trang 72)
Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.
Thảo luận (1)Hướng dẫn giảiTa cần chứng minh EFGH là hình chữ nhật. Thật vậy:
Do ABCD là hình thoi nên AB = BC = CD = DA.
Do E, H lần lượt là trung điểm của AB, AD nên AH = DH = AE = BE.
Tam giác AHE có AH = AE nên là tam giác cân tại A, suy ra \(\widehat {AHE} = \widehat {AEH}\)
Mà \(\widehat {HAE} + \widehat {AHE} + \widehat {AEH} = 180^\circ \)
Suy ra \(\widehat {AHE} = \frac{{180^\circ - \widehat {HAE}}}{2}\)
Tương tự, ta có tam giác DHG cân tại D nên \(\widehat {DHG} = \frac{{180^\circ - \widehat {HDG}}}{2}\)
Mặt khác, do ABCD là hình thoi nên AB // CD, suy ra \(\widehat {HAE} + \widehat {HDG} = 180^\circ \)
Khi đó \(\widehat {AHE} + \widehat {DHG} = \frac{{180^\circ - \widehat {HAE}}}{2} + \frac{{180^\circ - \widehat {HDG}}}{2}\)
= \(\frac{{180^\circ - \widehat {HAE} + 180^\circ - \widehat {HDG}}}{2}\)
=\(\frac{{360^\circ - (\widehat {HAE} + \widehat {HDG})}}{2}\)
= \(\frac{{360^\circ - 180^\circ }}{2}\)
Mà \(\widehat {AHE} + \widehat {DHG} + \widehat {EHG} = 180^\circ \)
Suy ra \(\widehat {EHG} = 180^\circ - (\widehat {AHE} + \widehat {DHG}) = 180^\circ - 90^\circ = 90^\circ \)
Chứng minh tương tự như trên ta cũng có \(\widehat {HEF} = \widehat {EFG} = \widehat {FGH} = {90^0}.\)
Tứ giác EFGH có bốn góc vuông nên là hình chữ nhật.
(Trả lời bởi Hà Quang Minh)
Bài 3.33 (SGK Kết nối tri thức với cuộc sống - Trang 72)
Cho hình chữ nhật ABCD có chu vi bằng 36 cm. Gọi M là trung điểm của cạnh BC. Biết rằng MA ⊥ MD. Tính độ dài các cạnh của hình chữ nhật ABCD (H.3.56).
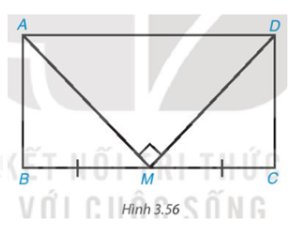
Thảo luận (1)Hướng dẫn giảiDo ABCD là hình chữ nhật nên \(\left\{{}\begin{matrix}AB=CD\\AD=BC\end{matrix}\right.\)
Mà M là trung điểm BC ⇒ \(\left\{{}\begin{matrix}MA=MD\\MB=MC\end{matrix}\right.\) (1)
Áp dụng định lí Py-ta-go trong tam giác ABM, MCD, AMD, ta có:
\(\left\{{}\begin{matrix}AB^2+MB^2=AM^2\\CD^2+MC^2=MD^2\\AM^2+MD^2=AD^2\end{matrix}\right.\) (2)
Từ (1) và (2), ta có:
\(2AB^2+2BM^2=AD^2=BC^2=4BM^2\)
\(\Rightarrow AB=BM=\dfrac{1}{2}BC\)
Mà \(2\cdot\left(AB+BC\right)=36\)
⇒ AB = 6 (cm) và BC = 12 (cm).
(Trả lời bởi Hà Quang Minh)