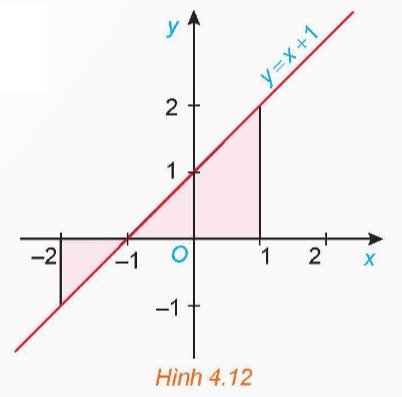
Xét hình phẳng giới hạn bởi đường thẳng y = f(x) = x + 1, trục hoành và hai đường thẳng x = −2; x = 1 (H.4.12).
a) Tính diện tích S của hình phẳng này.
b) Tính \(\int\limits^1_{-2}\left|f\left(x\right)\right|dx\) và so sánh với S.
Xét hình phẳng giới hạn bởi đường thẳng y = f(x) = x + 1, trục hoành và hai đường thẳng x = −2; x = 1 (H.4.12).
a) Tính diện tích S của hình phẳng này.
b) Tính \(\int\limits^1_{-2}\left|f\left(x\right)\right|dx\) và so sánh với S.

Tính diện tích hình phẳng giới hạn bởi parabol y = x2 – 4, trục hoành và hai đường thẳng x = 0; x = 3 (H.4.15).
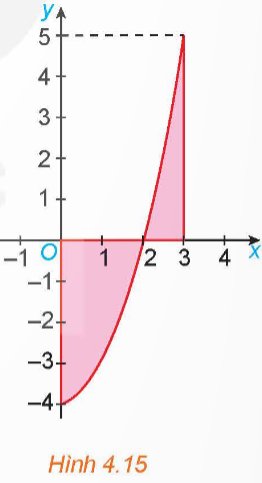
Thảo luận (1)Hướng dẫn giảiDiện tích hình phẳng cần tính là:
\(S = \int\limits_0^3 {\left| {{x^2} - 4} \right|dx} = \int\limits_0^2 {\left| {{x^2} - 4} \right|dx} + \int\limits_2^3 {\left| {{x^2} - 4} \right|dx} = - \int\limits_0^2 {\left( {{x^2} - 4} \right)dx} + \int\limits_2^3 {\left( {{x^2} - 4} \right)dx} \)
\( = - \left( {\frac{{{x^3}}}{3} - 4x} \right)\left| \begin{array}{l}2\\0\end{array} \right. + \left( {\frac{{{x^3}}}{3} - 4x} \right)\left| \begin{array}{l}3\\2\end{array} \right. = - \left( {\frac{{{2^3}}}{3} - 4.2} \right) + \left( {\frac{{{3^3}}}{3} - 4.3 - \frac{{{2^3}}}{3} + 4.2} \right) = \frac{{16}}{3} + \frac{7}{3} = \frac{{23}}{3}\)
(Trả lời bởi Nguyễn Quốc Đạt)
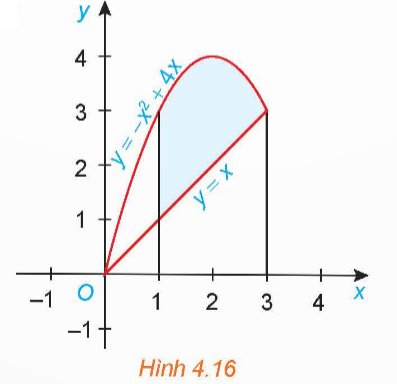
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số f(x) = −x2 + 4x, g(x) = x và hai đường thẳng x = 1, x = 3 (H.4.16).
a) Giả sử S1 là diện tích hình phẳng giới hạn bởi parabol y = −x2 + 4x, trục hoành và hai đường thẳng x = 1, x = 3; S2 là diện tích hình phẳng giới hạn bởi đường thẳng y = x, trục hoành và hai đường thẳng x = 1, x = 3. Tính S1, S2 và từ đó suy ra S.
b) Tính \(\int\limits^3_1\left|f\left(x\right)-g\left(x\right)\right|dx\) và so sánh với S.
Thảo luận (1)Hướng dẫn giảia) Diện tích hình phẳng giới hạn bởi parabol \(y = - {x^2} + 4x\), trục hoành và hai đường thẳng \(x = 1,x = 3\) là:
\({S_1} = \int\limits_1^3 {\left| { - {x^2} + 4x} \right|dx} = \int\limits_1^3 {\left( { - {x^2} + 4x} \right)dx} = \left( {\frac{{ - {x^3}}}{3} + 2{x^2}} \right)\left| \begin{array}{l}3\\1\end{array} \right. = \frac{{ - {3^3}}}{3} + {2.3^2} + \frac{1}{3} - {2.1^2} = \frac{{22}}{3}\)
Diện tích hình phẳng giới hạn bởi parabol \(y = x\), trục hoành và hai đường thẳng \(x = 1,x = 3\) là: \({S_2} = \int\limits_1^3 {\left| x \right|dx} = \int\limits_1^3 {xdx} = \frac{{{x^2}}}{2}\left| \begin{array}{l}3\\1\end{array} \right. = \frac{{{3^2}}}{2} - \frac{1}{2} = 4\)
Do đó, \(S = {S_1} - {S_2} = \frac{{22}}{3} - 4 = \frac{{10}}{3}\)
b) \(\int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} = \int\limits_1^3 {\left| { - {x^2} + 3x} \right|dx} = \int\limits_1^3 {\left( { - {x^2} + 3x} \right)dx} = \left( {\frac{{ - {x^3}}}{3} + \frac{{3{x^2}}}{2}} \right)\left| \begin{array}{l}3\\1\end{array} \right.\)
\( = \frac{{ - {3^3}}}{3} + \frac{{{{3.3}^2}}}{2} + \frac{1}{3} - \frac{3}{2} = \frac{{10}}{3}\)
Do đó, \(S = \int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
(Trả lời bởi Nguyễn Quốc Đạt)
Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = \(\sqrt{x}\), y = x – 2 và hai đường thẳng x = 1, x = 4.
Thảo luận (1)Hướng dẫn giảiDiện tích hình phẳng cần tính là:
\(\int\limits_1^4 {\left| {x - \sqrt x - 2} \right|dx} = - \int\limits_1^4 {\left( {x - \sqrt x - 2} \right)dx} = - \left( {\frac{{{x^2}}}{2} - \frac{{2x\sqrt x }}{3} - 2x} \right)\left| \begin{array}{l}4\\1\end{array} \right.\)
\( = - \left( {\frac{{{4^2}}}{2} - \frac{{2.4\sqrt 4 }}{3} - 2.4 - \frac{1}{2} + \frac{{2.1.\sqrt 1 }}{3} + 2.1} \right) = \frac{{19}}{6}\)
(Trả lời bởi Nguyễn Quốc Đạt)
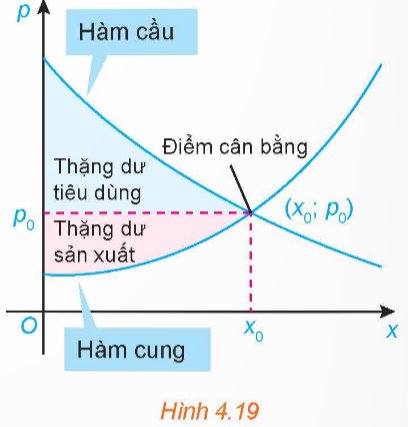
Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau (x0; p0) của đồ thị hàm cầu p = D(x) và đồ thị hàm cung p = S(x) được gọi là điểm cân bằng.
Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang p = p0 và đường thẳng đứng x = 0 là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang p = p0 và đường thẳng đứng x = 0 được gọi là thặng dư sản xuất, như trong Hình 4.19.
(Theo R.Larson, Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009).
Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:
Hàm cầu: p = −0,36x + 9 và hàm cung: p = 0,14x + 2, trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.
Thảo luận (1)Hướng dẫn giảiGọi điểm M là giao điểm của hàm cầu \(p = - 0,36x + 9\) và hàm cung \(p = 0,14x + 2\)
Khi đó, phương trình hoành độ giao điểm của hàm cầu và hàm cung là:
\( - 0,36x + 9 = 0,14x + 2\), suy ra \(x = 14\) nên \(p = - 0,36.14 + 9 = \frac{{99}}{{25}}\). Do đó, \(M\left( {14;\frac{{99}}{{25}}} \right)\)
Đồ thị hàm số \(p = - 0,36x + 9\) đi qua điểm \(M\left( {14;\frac{{99}}{{25}}} \right)\) và điểm N(0 ;9)
Đồ thị hàm số \(p = 0,14x + 2\) đi qua điểm \(M\left( {14;\frac{{99}}{{25}}} \right)\) và điểm P(0; 2)
Diện tích hình giới hạn bởi đồ thị hàm số \(p = - 0,36x + 9\), trục hoành và hai đường thẳng \(x = 0,x = 14\) là: \({S_1} = \int\limits_0^{14} {\left| { - 0,36x + 9} \right|dx} = \int\limits_0^{14} {\left( { - 0,36x + 9} \right)dx} = \left( { - 0,18{x^2} + 9x} \right)\left| \begin{array}{l}14\\0\end{array} \right.\)
\( = - 0,{18.14^2} + 9.14 = 90,72\)
Diện tích hình giới hạn bởi đồ thị hàm số \(p = 0,14x + 2\), trục hoành và hai đường thẳng \(x = 0,x = 14\) là:
\({S_2} = \int\limits_0^{14} {\left| {0,14x + 2} \right|dx} = \int\limits_0^{14} {\left( {0,14x + 2} \right)dx} = \left( {0,07{x^2} + 2x} \right)\left| \begin{array}{l}14\\0\end{array} \right.\)\( = 0,{07.14^2} + 2.14 = 41,72\)
Thặng dư tiêu dùng cho sản phẩm này là: \({S_1} - OQ.QM = 90,72 - 14.\frac{{99}}{{25}} = 35,28\)
Thặng dư sản xuất cho sản phẩm này là: \(OQ.OM - {S_2} = 14.\frac{{99}}{{25}} - 41,72 = 13,72\)
(Trả lời bởi Nguyễn Quốc Đạt)
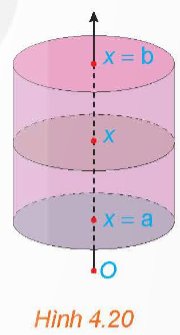
Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng x = a và x = b (a < b) (H.4.20).
a) Tính thể tích V của hình trụ.
b) Tính diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b). Từ đó tính \(\int\limits^b_aS\left(x\right)dx\) và so sánh với V.
Thảo luận (1)Hướng dẫn giảia) Thể tích V của hình trụ là: \(V = \pi {R^2}h = \pi {R^2}\left( {b - a} \right)\) (h là chiều cao của hình trụ)
b) Diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x là: \(S\left( x \right) = \pi {R^2}\).
Ta có: \(\int\limits_a^b {S\left( x \right)dx} = \int\limits_a^b {\pi {R^2}dx} = \pi {R^2}x\left| \begin{array}{l}b\\a\end{array} \right. = \pi {R^2}\left( {b - a} \right)\). Do đó, \(V = \int\limits_a^b {S\left( x \right)dx} \).
(Trả lời bởi Nguyễn Quốc Đạt)
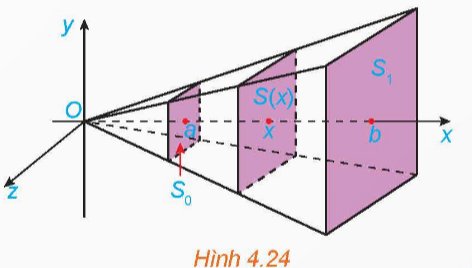
Tính thể tích của khối chóp cụt đều có diện tích hai đáy là S0, S1 và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.
Thảo luận (1)Hướng dẫn giảiTrong hệ trục tọa độ Oxyz, ta đặt khối chóp (tạo ra khối chóp cụt) sao cho đường cao nằm trên trục Ox và đỉnh trùng với gốc tọa độ.
Gọi a và b lần lượt là khoảng cách từ O đến đáy nhỏ và đáy lớn. Khi đó, chiều cao của khối chóp cụt là: \(h = b - a\).
Thiết diện của khối chóp cụt đều cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \(\left( {a \le x \le b} \right)\) là một đa giác đều đồng dạng với đáy lớn với tỉ số đồng dạng là \(\frac{x}{b}\).
Ta có: \(\frac{{S\left( x \right)}}{{{S_1}}} = \frac{{{x^2}}}{{{b^2}}}\) nên \(S\left( x \right) = {S_1}.\frac{{{x^2}}}{{{b^2}}}\).
Thể tích của khối chóp cụt đều là:
\(V = \int\limits_a^b {{S_1}\frac{{{x^2}}}{{{b^2}}}dx} = \frac{{{S_1}\left( {{b^3} - {a^3}} \right)}}{{3{b^2}}} = \frac{{b - a}}{3}.\frac{{{S_1}{a^2} + {S_1}ab + {S_1}{b^2}}}{{{b^2}}} = \frac{h}{3}\left( {\frac{{{S_1}{a^2}}}{{{b^2}}} + \frac{{{S_1}a}}{b} + {S_1}} \right)\)
Lại có: \({S_0} = S\left( a \right) = \frac{{{S_1}{a^2}}}{{{b^2}}},\frac{{{S_1}a}}{b} = \sqrt {{S_1}.\frac{{{S_1}{a^2}}}{{{b^2}}}} = \sqrt {{S_1}{S_0}} \). Do đó, \(V = \frac{h}{3}\left( {{S_0} + \sqrt {{S_0}{S_1}} + {S_1}} \right)\)
Khối chóp đều được coi là khối chóp cụt đều có \({S_0} = 0\). Do đó, thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h là: \(V = \frac{1}{3}S.h\).
(Trả lời bởi Nguyễn Quốc Đạt)
Xét hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left(x\right)=\dfrac{1}{2}x\), trục hoành và hai đường thẳng x = 0, x = 4. Khi quay hình phẳng này xung quanh trục hoành Ox ta được khối nón có đỉnh là gốc O, trục là Ox và đáy là hình tròn bán kính bằng 2 (H.4.25).
a) Tính thể tích V của khối nón.
b) Chứng minh rằng khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x (0 ≤ x ≤ 4) thì mặt cắt thu được là một hình tròn có bán kính là f(x), do đó diện tích mặt cắt là S(x) = πf2(x).
Tính \(\pi\int\limits^4_0f^2\left(x\right)dx\) và so sánh với V.
Thảo luận (1)Hướng dẫn giảia) Thể tích của khối nón là: \(V = \frac{1}{3}.\pi {.2^2}.4 = \frac{{16\pi }}{3}\)
b)
Khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x \(\left( {0 \le x \le 4} \right)\) thì mặt cắt thu được là một hình tròn có bán kính là \(f\left( x \right) = \frac{1}{2}x\).
Diện tích mặt cắt là: \(S\left( x \right) = \pi {f^2}\left( x \right) = \frac{1}{4}\pi {x^2}\).
Ta có: \(\pi \int\limits_0^4 {{f^2}\left( x \right)dx} = \pi \int\limits_0^4 {\frac{1}{4}{x^2}dx = \frac{{\pi {x^3}}}{{12}}\left| \begin{array}{l}4\\0\end{array} \right. = } \frac{{16\pi }}{3}\). Do đó, \(V = \pi \int\limits_0^4 {{f^2}\left( x \right)dx} \).
(Trả lời bởi Nguyễn Quốc Đạt)
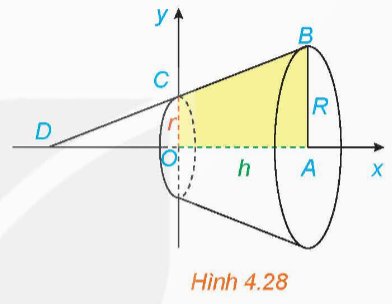
a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với OA = h, AB = R và OC = r, quanh trục Ox (H.4.28).
b) Từ công thức thu được ở phần a, hãy rút ra công thức tính thể tích của khối nón có bán kính đáy bằng R và chiều cao h.
Thảo luận (1)Hướng dẫn giảia)
Ta có: \(C\left( {0;r} \right),B\left( {h,R} \right) \Rightarrow \overrightarrow {BC} \left( { - h,r - R} \right) \Rightarrow \overrightarrow n \left( {r - R,h} \right)\)
Phương trình đường thẳng BC là: \(\left( {r - R} \right)x + h\left( {y - r} \right) = 0 \Leftrightarrow y = \frac{{hr + \left( {R - r} \right)x}}{h}\)
Thể tích hình cần tính là:
\(V = \pi \int\limits_0^h {{{\left[ {\frac{{hr + \left( {R - r} \right)x}}{h}} \right]}^2}dx} = \pi \int\limits_0^h {{{\left[ {r + \frac{{\left( {R - r} \right)x}}{h}} \right]}^2}dx} = \pi \int\limits_0^h {\left[ {{r^2} + \frac{{2r\left( {R - r} \right)x}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^2}}}{{{h^2}}}} \right]dx} \)
\( = \pi \left( {{r^2}x + \frac{{r\left( {R - r} \right){x^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^3}}}{{3{h^2}}}} \right)\left| \begin{array}{l}h\\0\end{array} \right. = \pi \left( {{r^2}h + \frac{{r\left( {R - r} \right){h^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{h^3}}}{{3{h^2}}}} \right)\)
\( = \pi \left( {{r^2}h + r\left( {R - r} \right)h + \frac{{{{\left( {R - r} \right)}^2}h}}{3}} \right) = \pi \left( {{r^2}h + rRh - {r^2}h + \frac{{{R^2}h}}{3} - \frac{{2rRh}}{3} + \frac{{{r^2}h}}{3}} \right)\)
\( = \pi \left( {\frac{{rRh}}{3} + \frac{{{R^2}h}}{3} + \frac{{{r^2}h}}{3}} \right) = \frac{1}{3}\pi h\left( {{R^2} + rR + {r^2}} \right)\)
b) Khi \(r = 0\) thì khối nón cụt trở thành khối nón có chiều cao h và bán kính đáy R. Do đó, thể tích khối nón là: \(V = \frac{1}{3}\pi {R^2}h\).
(Trả lời bởi Nguyễn Quốc Đạt)
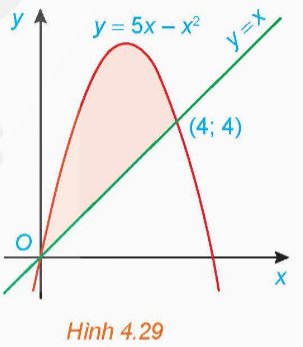
Tính diện tích của hình phẳng được tô màu trong Hình 4.29.
Thảo luận (1)Hướng dẫn giảiDiện tích hình phẳng cần tính là:
\(S = \int\limits_0^4 {\left| {5x - {x^2} - x} \right|dx} = \int\limits_0^4 {\left| { - {x^2} + 4x} \right|dx} = \int\limits_0^4 {\left( { - {x^2} + 4x} \right)dx} = \left( {\frac{{ - {x^3}}}{3} + 2{x^2}} \right)\left| \begin{array}{l}4\\0\end{array} \right. = \frac{{ - {4^3}}}{3} + {2.4^2} = \frac{{32}}{3}\)
(Trả lời bởi Nguyễn Quốc Đạt)