Bạn Ngân gấp một miếng bìa hình tam giác để các nếp gấp tạo thành ba tia phân giác của các góc ở đỉnh của tam giác đó (Hình 109).
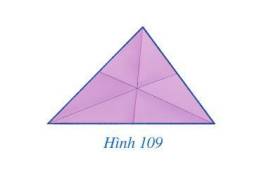
Ba nếp gấp đó có đặc điểm gì?
Bài 11. Tính chất ba đường phân giác của tam giác
Khởi động (SGK Cánh Diều trang 108)
Thảo luận (1)
Hoạt động 1 (SGK Cánh Diều trang 108,109)
Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D (Hình 110). Các đầu mút của đoạn thẳng AD có đặc điểm gì?
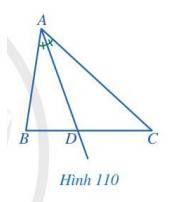
Thảo luận (1)Hướng dẫn giảiCác đầu mút của đoạn thẳng AD có đặc điểm: đầu mút A là đỉnh của tam giác, đầu mút D thuộc cạnh BC.
(Trả lời bởi Hà Quang Minh)
Luyện tập 1 (SGK Cánh Diều trang 108,109)
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung tuyến của tam giác đó.
Thảo luận (2)Hướng dẫn giải
Xét hai tam giác ABD và ACD:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\)(AD là phân giác của góc A);
AD chung.
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c).
Suy ra: BD = CD ( 2 cạnh tương ứng) hay D là trung điểm của cạnh BC. Vậy AD là đường trung tuyến của tam giác ABC.
(Trả lời bởi Kiều Sơn Tùng)
Hoạt động 2 (SGK Cánh Diều trang 109,110)
Quan sát các đường phân giác AD, BE, CK của tam giác ABC (Hình 114), cho biết ba đường phân giác đó có cùng đi qua một điểm hay không.
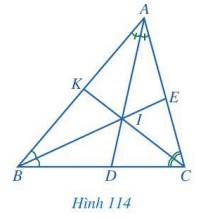
Thảo luận (2)Hướng dẫn giảiCác đường phân giác AD, BE, CK có cùng đi qua một điểm là điểm I
(Trả lời bởi Hà Quang Minh)
Luyện tập 2 (SGK Cánh Diều trang 109,110)
Tìm số đo x trong Hình 115.
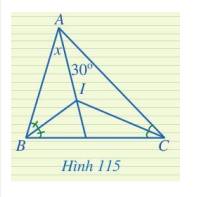
Thảo luận (1)Hướng dẫn giảiI là giao điểm của hai đường phân giác góc B và góc C.
Vậy I cũng là giao điểm của đường phân giác góc A với góc B và góc C.
Hay AI là phân giác của góc A. Vậy \(x = 30^\circ \).
(Trả lời bởi Hà Quang Minh)
Luyện tập 3 (SGK Cánh Diều trang 109,110)
Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.
Thảo luận (1)Hướng dẫn giải
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.
Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).
Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).
\(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).
Xét hai tam giác IDN và IDM có:
ID chung;
\(\widehat {NID} = \widehat {MID}\);
IN = IM.
Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)
\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);
\(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)
Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)
\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).
Suy ra: IC là đường trung trực của cạnh MN.
Tương tự ta có:
IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.
(Trả lời bởi Kiều Sơn Tùng)
Bài 1 (SGK Cánh Diều trang 111)
Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.
a) Các tam giác IMN, INP, IPM có là tam giác cân không? Vì sao?
b) Các tam giác ANP, BPM, CMN có là tam giác cân không? Vì sao?
Thảo luận (1)Hướng dẫn giải
a) Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Vậy các tam giác IMN, INP, IPM có là tam giác cân tại I.
b)
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông). Suy ra: CN = CM ( 2 cạnh tương ứng).
Vậy tam giác CMN có là tam giác cân.
Tương tự, ta có: AP = AN; BP = BM.
Vậy các tam giác ANP, BPM, CMN có là tam giác cân.
(Trả lời bởi Kiều Sơn Tùng)
Bài 2 (SGK Cánh Diều trang 111)
Tam giác ABC có ba đường phân giác cắt nhau tại I. Chứng minh:
a) \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \);
b) \(\widehat {BIC} = 90^\circ + \dfrac{1}{2}\widehat {BAC}\).
Thảo luận (1)Hướng dẫn giải
a) I là giao điểm của ba đường phân giác tại ba góc A, B, C nên:
\(\widehat {IAB} = \widehat {IAC};\widehat {IBA} = \widehat {IBC};\widehat {ICB} = \widehat {ICA}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = 180^\circ \\\widehat {IAB} + \widehat {IAC} + \widehat {IBA} + \widehat {IBC} + \widehat {ICB} + \widehat {ICA} = 180^\circ \\2\widehat {IAB} + 2\widehat {IBC} + 2\widehat {ICA} = 180^\circ \end{array}\)
Vậy \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \).
b) Tổng ba góc trong một tam giác bằng 180°. Xét tam giác BIC:
\(\begin{array}{l}\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ \\\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\end{array}\).
Mà \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \)→ \(\widehat {IBC} + \widehat {ICA} = 90^\circ - \widehat {IAB}\).
Vậy: \(\begin{array}{l}\widehat {BIC} = 180^\circ - (\widehat {IBC} + \widehat {ICB})\\\widehat {BIC} = 180^\circ - (90^\circ - \widehat {IAB})\\\widehat {BIC} = 90^\circ + \widehat {IAB}\end{array}\)
Mà \(\widehat {IAB} = \dfrac{1}{2}\widehat {BAC}\)(IA là phân giác của góc BAC).
Vậy \(\widehat {BIC} = 90^\circ + \widehat {IAB} = 90^\circ + \dfrac{1}{2}\widehat {BAC}\).
(Trả lời bởi Kiều Sơn Tùng)
Bài 3 (SGK Cánh Diều trang 111)
Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC.
a) Chứng minh \(\widehat {CBI} > \widehat {ACI}\);
b) So sánh IB và IC.
Thảo luận (1)Hướng dẫn giải
a) Ta có: AB < AC nên \(\widehat {ABC} > \widehat {ACB}\)(góc ABC đối diện với cạnh AC; góc ACB đối diện với cạnh AB).
Mà BI và CI là hai đường phân giác của góc ABC và góc ACB nên: \(\widehat {CBI} > \widehat {ACI}\)
(Vì: \(\widehat {CBI} = \dfrac{1}{2}\widehat {ABC};\widehat {ACI} = \dfrac{1}{2}\widehat {ACB}\)).
b) Ta có: \(\widehat {ACI} = \widehat {BCI}\)
Mà \(\widehat {CBI} > \widehat {ACI}\) ( câu a)
Do đó \(\widehat {CBI} > \widehat {BCI}\).
Mà IC đối diện với góc CBI; IB đối diện với góc BCI.
Vậy IC > IB (cạnh đối diện với góc lớn hơn thì có số đo độ dài lớn hơn).
(Trả lời bởi Kiều Sơn Tùng)
