Cho hàm số \(y = \frac{2}{3}{x^2}\). Hãy tính giá trị của y khi:
a) \(x = - 3\)
b) \(x = 0\)
c) \(x = 3\)
Cho hàm số \(y = \frac{2}{3}{x^2}\). Hãy tính giá trị của y khi:
a) \(x = - 3\)
b) \(x = 0\)
c) \(x = 3\)
Hàm số nào sau đây có dạng \(y = a{x^2}(a \ne 0)\)? Đối với những hàm số đó, xác định hệ số a của \({x^2}\).
a) \(y = - {x^2}\)
b) \(y = \frac{{{x^2}}}{2}\)
c) \(y = \frac{1}{{4{x^2}}}\)
Thảo luận (1)Hướng dẫn giảiCác hàm số có dạng \(y = a{x^2}(a \ne 0)\) là:
a) \(y = - {x^2}\), với \(a = - 1\)
b) \(y = \frac{{{x^2}}}{2}\), với \(a = \frac{1}{2}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hàm số \(y = a{x^2}\). Tìm a, biết rằng khi \(x = - 3\) thì \(y = 5\).
Thảo luận (1)Hướng dẫn giảiThay \(x = - 3\) và \(y = 5\) vào hàm số \(y = a{x^2}\) ta được:
\(\begin{array}{l}5 = a{( - 3)^2}\\9a = 5\\a = \frac{5}{9}\end{array}\)
Vậy \(a = \frac{5}{9}\)
(Trả lời bởi Nguyễn Quốc Đạt)
a) Nêu khái niệm đồ thị của hàm số \(y = f(x)\).
b) Xét hàm số \(y = 2{x^2}\). Hãy thực hiện các hoạt động sau:
- Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

- Trên mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ như trong bảng giá trị trên.
- Quan sát Hình 1, vẽ đường cong như ở Hình 1 đi qua 5 điểm A, B, O, C, D. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị của hàm số \(y = 2{x^2}\).

c) Xét hàm số \(y = - 2{x^2}\). Hãy thực hiện các hoạt động sau:
- Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:
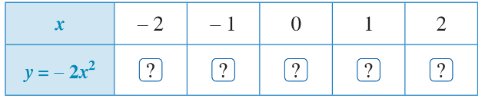
- Trên mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ như trong bảng giá trị trên.
- Quan sát Hình 2, vẽ vẽ đường cong như ở Hình 2 đi qua 5 điểm M, N, O, P, Q. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị của hàm số \(y = - 2{x^2}\).

Thảo luận (1)Hướng dẫn giảia) Đồ thị của hàm số \(y = f(x)\) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng \((x;f(x))\) trên mặt phẳng tọa độ.
b)
Các điểm A(-2;8), B(-1;2), O(0;0), C(1;2), D(2;8)
Đồ thị của hàm số \(y = 2{x^2}\):
c)
Các điểm A(-2;-8), B(-1;-2), O(0;0), C(1;-2), D(2;-8)
Đồ thị của hàm số \(y = - 2{x^2}\):
(Trả lời bởi Nguyễn Quốc Đạt)
Quan sát đồ thị của hàm số \(y = \frac{1}{2}{x^2}\) ở Hình 4, hãy nêu nhận xét về vị trí cặp điểm E và H, F và G đối với trục Oy.

Thảo luận (1)Hướng dẫn giảiĐiểm E đối xứng với H, F đối xứng với G qua Oy.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hàm số \(y = \frac{1}{3}{x^2}\).
a) Tìm giá trị của y tương ứng với giái trị của x trong bảng sau:

b) Dựa vào bảng giá trị trên, vẽ đồ thị của hàm số đó.
c) Tìm những điểm thuộc đồ thị của hàm số có hoành độ lần lượt bằng -6; 10.
d) Tìm những điểm thuộc đồ thị của hàm số có tung độ bằng 27.
Thảo luận (1)Hướng dẫn giảia) Ta có bảng giá trị sau:
b) Đồ thị hàm số \(y = \frac{1}{3}{x^2} \) là một parabol đi qua các điểm \(A(-3;3); B(-2;\frac{4}{3}); O(0;0); C(2;\frac{4}{3}); D(3;3)\)
c) Thay \(x = - 6\) vào hàm số \(y = \frac{1}{3}{x^2}\) ta được:
\(y = \frac{1}{3}{( - 6)^2} \Leftrightarrow y = 12\).
Ta có điểm (-6; 12) thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\).
Thay \(x = 10\) vào hàm số \(y = \frac{1}{3}{x^2}\) ta được:
\(y = \frac{1}{3}{(10)^2} \Leftrightarrow y = \frac{{100}}{3}\).
Ta có điểm \(\left( {10;\frac{{100}}{3}} \right)\) thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\).
d) Thay \(y = 27\) vào hàm số \(y = \frac{1}{3}{x^2}\) ta được:
\(27 = \frac{1}{3}{x^2} \Leftrightarrow {x^2} = 81 \Leftrightarrow x = \pm 9\).
Ta có điểm \(\left( { - 9;27} \right),\left( {9;27} \right)\) thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hàm số \(y = a{t^2}\) biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125m sau khoảng thời gian là 5 giây.
a) Tìm hệ số a.
b) Vẽ đồ thị của hàm số.
Thảo luận (1)Hướng dẫn giảia) Vì chiếc xe đua đi được 125 m sau khoảng thời gian là 5 giây nên ta có: y = 125 và t = 5.
Thay y = 125 và t = 5 vào hàm số y = at2, ta có:
125 = a.52 hay 25a = 125. Suy ra a = 5.
Vậy a = 5.
b) Với a = 5 ta có hàm số sau: y = 5t2.
– Ta có bảng giá trị của y tương ứng với giá trị của t như sau:
– Vẽ các điểm A(–1; 5); \(B\left(-\dfrac{1}{2};\dfrac{5}{4}\right);O\left(0;0\right);C\left(\dfrac{1}{2};\dfrac{5}{4}\right)\); D(1; 5) thuộc đồ thị hàm số y = 5t2 trong mặt phẳng tọa độ Oty.
– Vẽ đường parabol đi qua 5 điểm A, B, O, C, D, ta nhận được đồ thị của hàm số y = 5t2 (hình vẽ).
(Trả lời bởi Nguyễn Quốc Đạt)
Cá heo có thể nhảy cao tới 25 feet và thực hiện các thủ thuật như nhảy qua vòng, lộn nhào trong không trung. Giả sử quỹ đạo nhảy của cá heo là parabol \(y = a{x^2}\), với gốc tọa độ là vị trí cao nhất mà cá heo đạt được, cách mặt nước 25 feet, trong đó y được tính theo đơn vị feet và x được tính theo đơn vị giây (Hình 6). Biết rằng sau 2 giây kể từ vị trí cao nhất đó, cá heo rơi chạm mặt nước. tìm hàm số biểu thị quỹ đạo nhảy của cá heo.

Thảo luận (1)Hướng dẫn giảiTa thấy quỹ đạo nhảy của cá heo là parabol có vị trí cao nhất là O(0;0) suy ra đồ thị nằm bên dưới trục hoành và y = -25 và x = 2.
Thay y = -25 và x = 2 vào hàm số \(y = a{x^2}\) ta được: \( - 25 = a{.2^2} \Leftrightarrow a = \frac{{ - 25}}{4}\)
Vậy hàm số biểu thị quỹ đạo nhảy của cá heo có dạng \(y = \frac{{ - 25}}{4}{x^2}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Trên mặt phẳng tọa độ Oxy, điểm M(2;-1) thuộc đồ thị hàm số \(y = a{x^2}\).
a) Tìm hệ số a.
b) Điểm A(4;-4) có thuộc đồ thị hàm số hay không?
c) Hãy tìm một số điểm (không kể điểm O) thuộc đồ thị hàm số, rồi vẽ đồ thị của hàm số.
Thảo luận (1)Hướng dẫn giảia) Vì đồ thị hàm số đi qua điểm $M(2 ;-1)$ nên $x=2, y=-1$ thỏa mãn hàm số $y=a x^2$.
Thay $\mathrm{x}=2, \mathrm{y}=-1$ vào hàm số $\mathrm{y}=\mathrm{ax}^2$, ta được:
$-1=$ a. $2^2$ hay $4 a=-1$, suy ra $a=-\frac{1}{4}$
Vậy $a=-\frac{1}{4}$.
b) Với $a=-\frac{1}{4}$ ta có hàm số $y=-\frac{1}{4} x^2$.Xét điểm $\mathrm{A}(4 ;-4)$ : Do $-4=-\frac{1}{4} \cdot 4^2$ nên điểm $\mathrm{A}(4 ;-4)$ thuộc đồ thị hàm số $y=-\frac{1}{4} x^2$.
c) Xét hàm số $y=-\frac{1}{4} x^2$.
- Ta có bảng giá trị của y tương ứng với giá trị của x như sau:
- Vẽ các điểm $B(-4 ;-4) ; C(-2 ;-1) ; O(0 ; 0) ; D(2 ;-1) ; A(4 ;-4)$ thuộc đồ thị hàm số $y=-\frac{1}{4} x^2$ trong mặt phẳng tọa độ Oxy.
- Vẽ đường parabol đi qua 5 điểm $\mathrm{A}, \mathrm{B}, \mathrm{O}, \mathrm{C}, \mathrm{D}$, ta nhận được đồ thị của hàm số $y=-\frac{1}{4} x^2$ (hình vẽ).(Trả lời bởi Nguyễn Quốc Đạt)
Vẽ đồ thị của hàm số \(y = - 3{x^2}\).
Thảo luận (1)Hướng dẫn giải– Ta có bảng giá trị của y tương ứng với giá trị của x như sau:
– Vẽ các điểm A(–2; –12); B(–1; –3); O(0; 0); C(1; –3); D(2; –12) thuộc đồ thị hàm số y = –3x2 trong mặt phẳng tọa độ Oxy.
– Vẽ đường parabol đi qua 5 điểm A, B, O, C, D, ta nhận được đồ thị của hàm số y = –3x2 (hình vẽ).
(Trả lời bởi Nguyễn Quốc Đạt)