a) Vì đồ thị hàm số đi qua điểm $M(2 ;-1)$ nên $x=2, y=-1$ thỏa mãn hàm số $y=a x^2$.
Thay $\mathrm{x}=2, \mathrm{y}=-1$ vào hàm số $\mathrm{y}=\mathrm{ax}^2$, ta được:
$-1=$ a. $2^2$ hay $4 a=-1$, suy ra $a=-\frac{1}{4}$
Vậy $a=-\frac{1}{4}$.
b) Với $a=-\frac{1}{4}$ ta có hàm số $y=-\frac{1}{4} x^2$.
Xét điểm $\mathrm{A}(4 ;-4)$ : Do $-4=-\frac{1}{4} \cdot 4^2$ nên điểm $\mathrm{A}(4 ;-4)$ thuộc đồ thị hàm số $y=-\frac{1}{4} x^2$.
c) Xét hàm số $y=-\frac{1}{4} x^2$.
- Ta có bảng giá trị của y tương ứng với giá trị của x như sau: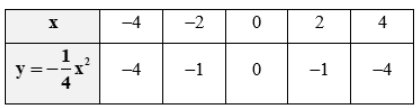
- Vẽ các điểm $B(-4 ;-4) ; C(-2 ;-1) ; O(0 ; 0) ; D(2 ;-1) ; A(4 ;-4)$ thuộc đồ thị hàm số $y=-\frac{1}{4} x^2$ trong mặt phẳng tọa độ Oxy.
- Vẽ đường parabol đi qua 5 điểm $\mathrm{A}, \mathrm{B}, \mathrm{O}, \mathrm{C}, \mathrm{D}$, ta nhận được đồ thị của hàm số $y=-\frac{1}{4} x^2$ (hình vẽ).



