15 phút = \(\dfrac{{15}}{{60}}\) giờ = \(\dfrac{{15:15}}{{60:15}}\) giờ = \(\dfrac{1}{4}\) giờ
90 phút =\(\dfrac{{90}}{{60}}\) giờ = \(\dfrac{{90:30}}{{60:30}}\) giờ = \(\dfrac{3}{2}\) giờ.
Trong các phân số \(\dfrac{{11}}{{23}};\dfrac{{ - 24}}{{15}}\), phân số nào là phân số tối giản? Nếu chưa là phân số tối giản, hãy rút gọn chúng.
Viết kết quả của các phép chia sau dưới dạng phân số:
a) \(4:9\)
b) \((-2):7\)
c) \(8: (-3)\)
Các cặp phân số sau đây có bằng nhau không?
a) \(\dfrac{{ - 3}}{5}\) và \(\dfrac{9}{{ - 15}}\)
b) \(\dfrac{{ - 1}}{{ - 4}}\) và \(\dfrac{1}{4}\)
Viết mỗi phân số sau đây thành phân số bằng nó và có mẫu dương
\(\dfrac{8}{{ - 11}};\dfrac{-5}{{ - 9}}\)
Cách viết nào sau đây cho ta một phân số? Cho biết tử và mẫu của phân số đó.
\(\dfrac{{ - 2,5}}{4};\dfrac{0}{7};\dfrac{3}{{ - 8}};\dfrac{4}{0}\)
a) Cho biết các phân số sau có bằng nhau không?
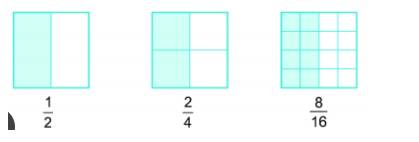
b) Thay các dấu “?” trong hình dưới bằng số thích hợp rồi rút ra nhận xét.
Tìm những cặp phân số bằng nhau trong các phân số sau và sử dụng tính chất cơ bản của phân số đề giải thích kết luận.
\(\dfrac{1}{5};\dfrac{{ - 10}}{{55}};\dfrac{3}{{15}};\dfrac{{ - 2}}{{11}}\)
Viết phân số biểu thị phần tô màu trong mỗi hình dưới.
Một vòi nước chảy vào một bể không có nước, sau 40 phút thì đầy bể. Hỏi sau 10 phút, lượng nước đã chảy chiếm bao nhiêu phần bể?
