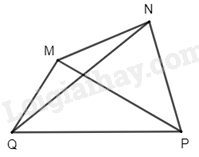
- Hai đỉnh đối nhau là: \(M\) và \(P\); \(Q\) và \(N\)
- Hai đường chéo là: \(MP\) và \(QN\)
- Hai cạnh đối nhau là: \(MN\) và \(PQ\); \(MQ\) và \(NP\)

- Hai đỉnh đối nhau là: \(M\) và \(P\); \(Q\) và \(N\)
- Hai đường chéo là: \(MP\) và \(QN\)
- Hai cạnh đối nhau là: \(MN\) và \(PQ\); \(MQ\) và \(NP\)
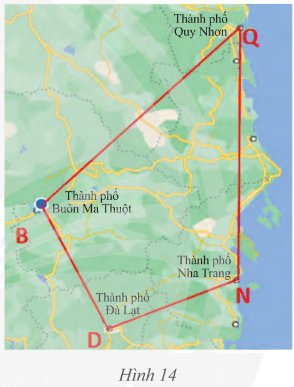
Trên bản đồ, tứ giác \(BDNQ\) với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.
a) Tìm các cạnh kề và cạnh đối diện của cạnh \(BD\).
b) Tìm các đường chéo của tứ giác
Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên \(CHRL\) (Hình 6)

Vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác sau đây và nêu nhận xét của em về vị trí của mỗi tứ giác đối với mỗi đường thẳng đã vẽ.
Đường chéo \(AC\) chia tứ giác \(ABCD\) thành hai tam giác \(ACB\) và \(ACD\) (Hình 7). Tính tổng các góc của tam giác \(ACB\) và tam giác \(ACD\). Từ đó, ta có nhận xét gì về tổng các góc của tứ giác \(ABCD\) .

Tứ giác \(ABCD\) có góc ngoài tại đỉnh \(A\) bằng \(65^\circ \), góc ngoài tại đỉnh \(B\) bằng \(100^\circ \), góc ngoài tại đỉnh \(C\) bằng \(60^\circ \). Tính số đo góc ngoài tại đỉnh \(D\).
Tứ giác \(ABCD\) có \(\widehat A = 100^\circ \), góc ngoài tại đỉnh \(B\) bằng \(110^\circ \), \(\widehat C = 75^\circ \). Tính số đo góc \(D\)
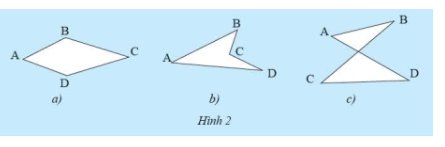
Trong các hình tạo bởi bốn đoạn thẳng \(AB\), \(BC\), \(CD\) và \(DA\) sau đây, hình nào không có hai đoạn thẳng cùng nằm trên một đường thẳng?
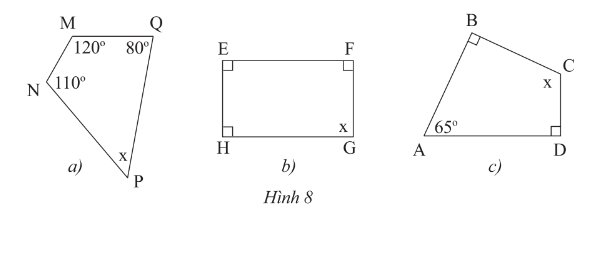
Tìm \(x\) trong mỗi tứ giác sau:
Ta gọi tứ giác ABCD với AB = AD, CB = CD (hình 13) là hình “cái diều”.
a. Chứng minh rằng AC là đường trung trực của BD.
b. Cho biết \(\widehat B = {95^0},\widehat C = {35^0}.\)Tính \(\widehat A\) và \(\widehat D\)