Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy điểm O và vẽ các vectơ\(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Lấy điểm O’ khác O và vẽ các vectơ \(\overrightarrow {O'A'} = \overrightarrow a ,\overrightarrow {O'B'} = \overrightarrow b \) (H.2.21).
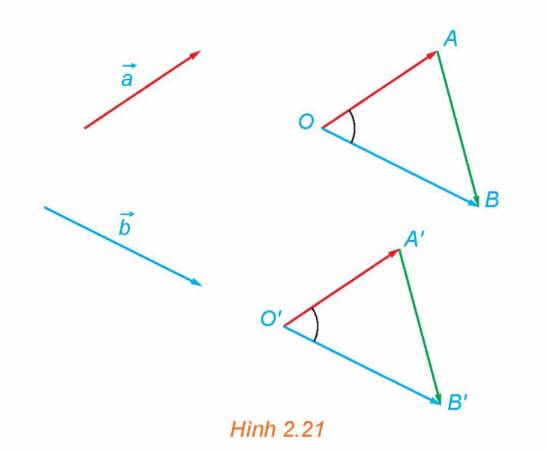
a) Ta có: \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} ;\overrightarrow {A'B'} = \overrightarrow {A'O'} + \overrightarrow {O'B'} \)
Mà \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {O'A'} = \overrightarrow a ,\overrightarrow {O'B'} = \overrightarrow b \Rightarrow \overrightarrow {AO} = \overrightarrow {A'O'} ;\overrightarrow {OB} = \overrightarrow {O'B'} \)
Do đó, \(\overrightarrow {AB} = \overrightarrow {A'B'} \)
b) Áp dụng định lí côsin vào tam giác AOB ta có: \(\cos \widehat {AOB} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)
Áp dụng định lí côsin vào tam giác A’O’B’ ta có: \(\cos \widehat {A'O'B'} = \frac{{O'A{'^2} + O'B{'^2} - A'B{'^2}}}{{2.O'A'.O'B'}}\)
Vì \(\overrightarrow {AB} = \overrightarrow {A'B'} \Rightarrow AB = A'B',\overrightarrow {AO} = \overrightarrow {A'O'} \Rightarrow OA = O'A'\overrightarrow {OB} = \overrightarrow {O'B'} \Rightarrow OB = O'B'\)
Do đó, \(\cos \widehat {AOB} = \cos \widehat {A'O'B'} \Rightarrow \widehat {AOB} = \widehat {A'O'B'}\)




