mk giải vs ĐK nhé: Rv = \(\infty\); Ra = 0
Khi k đóng:
((R2 //R3)ntR4)//R1
\(\Rightarrow R_{234}=\dfrac{R_2.R_3}{R_2+R_3}+R_4=0,5+1=1,5\left(\Omega\right)\)
\(\Rightarrow I_1=\dfrac{U}{R_1}=\dfrac{U}{1}\)
\(\rightarrow I_{234}=\dfrac{U_{234}}{R_{234}}=\dfrac{U}{1,5}=\dfrac{2U}{3}\)
\(\Rightarrow U_2=U_3=U_{23}=\dfrac{\dfrac{2U}{3}}{0,5}=\dfrac{4}{3}U\)
\(\Rightarrow I_2=\dfrac{U_2}{R_2}=\dfrac{\dfrac{4U}{3}}{1}=\dfrac{4}{3}U\)
Đong điện đi từ C -> D, Xét nút C.
\(I_A=I_1+I_2=\dfrac{4}{3}U+U=1\)
\(\Rightarrow U\approx0,43\left(V\right)\)
TH2 : k mở
\
\(R_{tđ}=R_3+\dfrac{\left(R_2+R_1\right)R_4}{R_2+R_1+R_4}=1+\dfrac{2.1}{2+1}=\dfrac{5}{3}\left(\Omega\right)\)
\(\Rightarrow I_3=I_{124}=\dfrac{U}{R_{tđ}}=\dfrac{4,3}{\dfrac{5}{3}}=2,58\left(A\right)\)
\(\Rightarrow U_3=2,58.1=2,58\left(V\right)\)
\(\Rightarrow U_{124}=4,3-2,58=1,72\left(V\right)\)
\(\Rightarrow I_{12}=I_1=I_2=\dfrac{U_{124}}{R_{12}}=\dfrac{1,72}{0,5}=3,44\left(A\right)\)
\(\Rightarrow U_2=3,44.1=3,44\left(V\right)\)
Nút C: \(U_V=U_2-U_3=3,44-2,5=0,94\left(V\right)\)
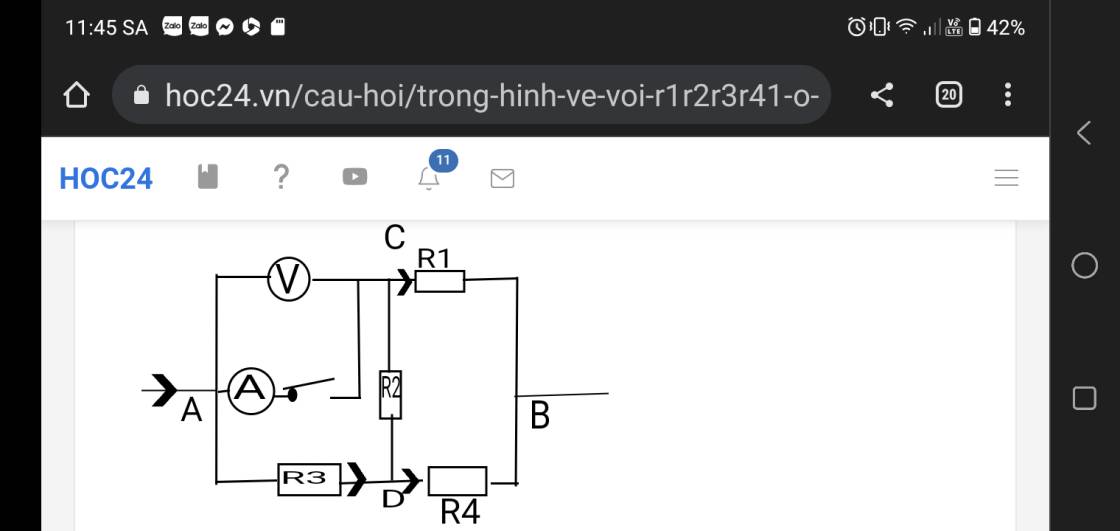
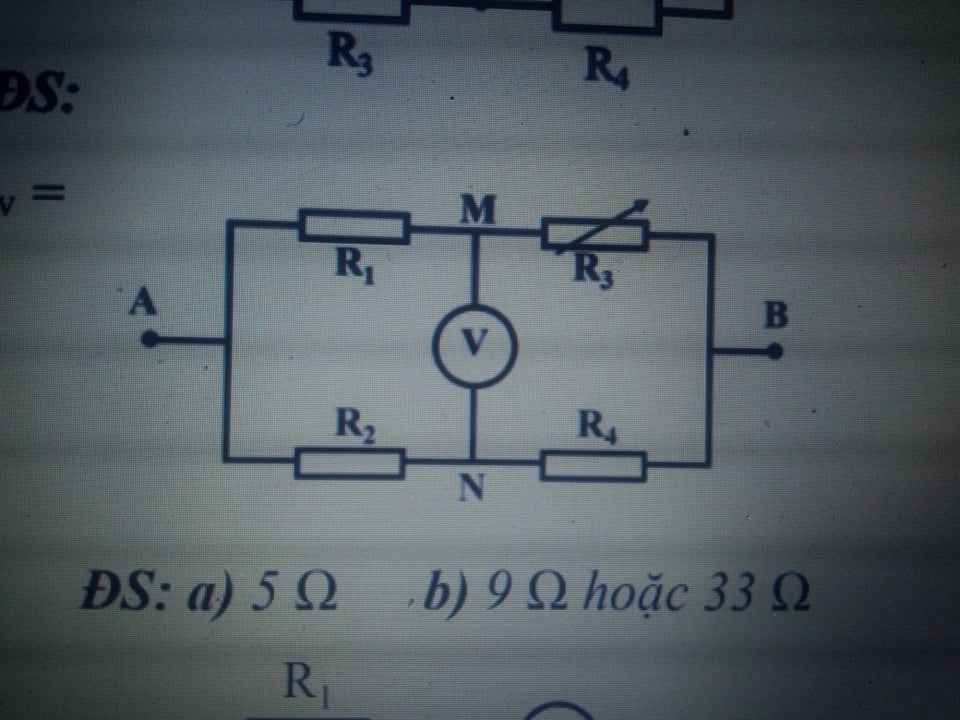
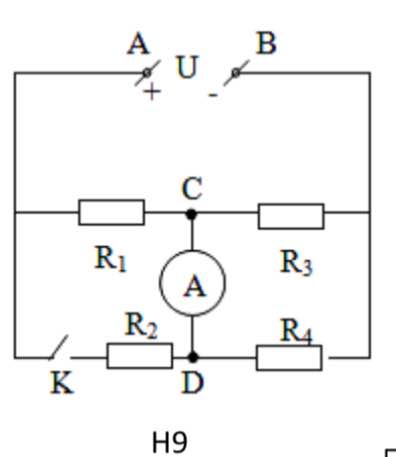
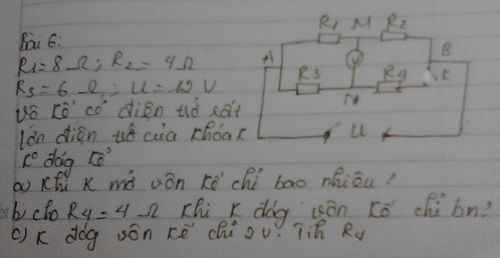Mình thay đổi số liệu như dưới nhé:
