Vì tổng số đo 3 góc trong tam giác là \({180^o}\)
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
Mà \(\widehat B = \widehat C\)\( = ({180^o} - \widehat A):2\)\( = ({180^o} - {110^o}):2 = {35^o}\)
Vì tổng số đo 3 góc trong tam giác là \({180^o}\)
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
Mà \(\widehat B = \widehat C\)\( = ({180^o} - \widehat A):2\)\( = ({180^o} - {110^o}):2 = {35^o}\)
Cho tam giác ABC có \(\widehat A\)=\(\widehat C\). Vẽ đường thẳng đi qua điểm B, vuông góc với AC và cắt AC tại điểm H (Hình 9). Em hãy làm theo gợi ý sau để chứng minh BA = BC.
Xét \(\Delta AHB\)và \(\Delta CHB\)cùng vuông tại H, ta có:
BH là cạnh góc vuông ?
\(\widehat {HAB}\) = \(\widehat {HCB}\) suy ra \(\widehat {ABH} = \widehat {CBH}\) (?)
Vậy \(\Delta AHB = \Delta CHB\). Suy ra BA = BC

Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E.
a) Chứng minh rẳng \(\widehat {ABF} = \widehat {ACE}\)
b) Chứng minh rằng tam giác AEF cân
c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và tam giác IEF là những tam giác cân
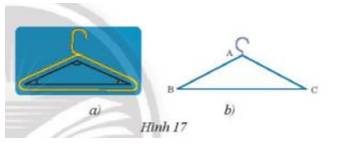
Phần thân của một móc treo quần áo có dạng hình tam giác cân (Hình 17a) được vẽ lại như Hình 17b. Cho biết AB = 20 cm; BC = 28 cm và \(\widehat B\)= 35°. Tìm số đo các góc còn lại và chu vi của tam giác ABC.
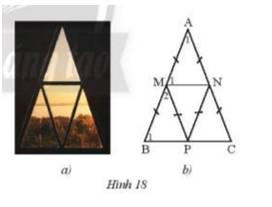
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.
a) Cho biết \(\widehat {{A_1}}\)\( = {42^o}\). Tính số đo của \(\widehat {{M_1}}\),\(\widehat {{B_1}}\),\(\widehat {{M_2}}\).
b) Chứng minh MN // BC, MP // AC.
c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.
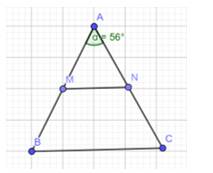
Cho tam giác ABC cân tại A có \(\widehat A = {56^o}\)(Hình 15)
a) Tính\(\widehat B\), \(\widehat C\)
b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.
c) Chứng minh rằng MN // BC
Tìm các tam giác cân trong Hình 4. Kể tên các cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của mỗi tam giác cân đó.
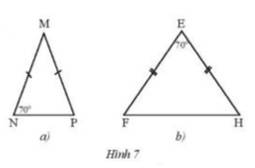
Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7.
Cho Hình 14, biết ED = EF và EI là tia phân giác của \(\widehat {DEF}\)

Chứng minh rằng:
a) \(\Delta EID = \Delta EIF\)
b) Tam giác DIF cân
Cho tam giác ABC cân tại A (Hình 5). Gọi M là trung điểm cạnh BC. Nối A với M. Em hãy làm theo gợi ý sau để chứng minh \(\widehat {ABC}\)=\(\widehat {ACB}\).
Xét \(\Delta AMB\) và \(\Delta AMC\)có:
AB = ? (?)
MB = MC (?)
AM là cạnh ?
Vậy \(\Delta AMB\) =\(\Delta AMC\) (c.c.c)
Suy ra \(\widehat {ABC}\)=\(\widehat {ACB}\)
