Em hãy đo rồi so sánh độ dài hai cạnh AB và AC của tam giác ABC có trong hình di tích ga xe lửa Đà Lạt dưới đây.

Em hãy đo rồi so sánh độ dài hai cạnh AB và AC của tam giác ABC có trong hình di tích ga xe lửa Đà Lạt dưới đây.

Gấp đôi một tờ giấy hình chữ nhật ABCD theo đường gấp MS. Cắt hình gấp được theo đường chép AS rồi trải phẳng hình cắt được ra ta có tam giác SAB (Hình 1). Em hãy so sánh hai cạnh SA và SB của tam giác này.
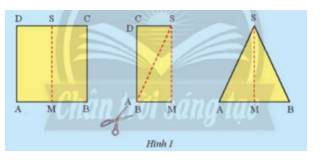
Thảo luận (1)Hướng dẫn giảiTa thấy sau khi cắt 2 cạnh của tam giác bằng nhau
(Trả lời bởi Hà Quang Minh)
Tìm các tam giác cân trong Hình 4. Kể tên các cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của mỗi tam giác cân đó.
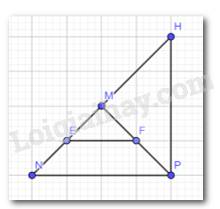
Thảo luận (1)Hướng dẫn giảiTa thấy: \(\Delta MEF\)cân tại M do ME = MF có:
+ cạnh bên: ME, MF
+ cạnh đáy: EF
+ góc ở đỉnh: \(\widehat {EMF}\)
+ góc ở đáy: \(\widehat {MEF}\),\(\widehat {MFE}\)
\(\Delta MNP\) cân tại M do MN = MP có:
+ cạnh bên: MN, MP
+ cạnh đáy: NP
+ góc ở đỉnh: \(\widehat {NMP}\)
+ góc ở đáy: \(\widehat {NPM}\), \(\widehat {PNM}\)
\(\Delta MHP\) cân tại M do MH = MP có:
+ cạnh bên : MH, MP
+ cạnh đáy: HP
+ góc ở đỉnh: \(\widehat {PMH}\)
+ góc ở đáy: \(\widehat {MPH}\),\(\widehat {MHP}\)
(Trả lời bởi Hà Quang Minh)
Cho tam giác ABC cân tại A (Hình 5). Gọi M là trung điểm cạnh BC. Nối A với M. Em hãy làm theo gợi ý sau để chứng minh \(\widehat {ABC}\)=\(\widehat {ACB}\).
Xét \(\Delta AMB\) và \(\Delta AMC\)có:
AB = ? (?)
MB = MC (?)
AM là cạnh ?
Vậy \(\Delta AMB\) =\(\Delta AMC\) (c.c.c)
Suy ra \(\widehat {ABC}\)=\(\widehat {ACB}\)

Thảo luận (1)Hướng dẫn giảiXét \(\Delta AMB\) và \(\Delta AMC\).có:
AB = AC ( do tam giác ABC cân tại A )
MB = MC ( do M là trung điểm BC )
AM là cạnh chung
=>\(\Delta AMB\) =\(\Delta AMC\) (c.c.c)
=>\(\widehat {ABC}\)=\(\widehat {ACB}\)( 2 góc tương ứng)
(Trả lời bởi Hà Quang Minh)
Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7.
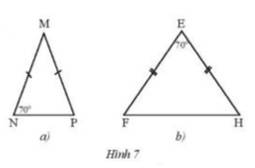
Thảo luận (1)Hướng dẫn giảia) Vì \(\Delta MNP\) cân tại M ( theo giả thiết )
\( \Rightarrow \widehat N = \widehat P = {70^o}\) ( 2 góc đáy của tam giác cân )
\( \Rightarrow \widehat M = {180^o} - {2.70^o} = {40^o}\)
b) Xét \(\Delta EFH\) cân tại E
Theo định lí về tổng 3 góc trong tam giác ta có
\( \Rightarrow \widehat E + \widehat F + \widehat H = {180^o}\)
Mà \(\widehat F = \widehat H\)( tính chất tam giác cân )
\( \Rightarrow \widehat F = \widehat H = {180^o} - \widehat E = ({180^o} - {70^o}):2 = {55^o}\)
(Trả lời bởi Hà Quang Minh)
Trong hình mái nhà ở Hình 8, tính góc B và góc C, biết \(\widehat A\)= \({110^o}\).

Thảo luận (1)Hướng dẫn giảiVì tổng số đo 3 góc trong tam giác là \({180^o}\)
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
Mà \(\widehat B = \widehat C\)\( = ({180^o} - \widehat A):2\)\( = ({180^o} - {110^o}):2 = {35^o}\)
(Trả lời bởi Hà Quang Minh)
Cho tam giác ABC có \(\widehat A\)=\(\widehat C\). Vẽ đường thẳng đi qua điểm B, vuông góc với AC và cắt AC tại điểm H (Hình 9). Em hãy làm theo gợi ý sau để chứng minh BA = BC.
Xét \(\Delta AHB\)và \(\Delta CHB\)cùng vuông tại H, ta có:
BH là cạnh góc vuông ?
\(\widehat {HAB}\) = \(\widehat {HCB}\) suy ra \(\widehat {ABH} = \widehat {CBH}\) (?)
Vậy \(\Delta AHB = \Delta CHB\). Suy ra BA = BC

Thảo luận (1)Hướng dẫn giảiXét \(\Delta AHB\) và \(\Delta CHB\) cùng vuông tại H, ta có:
BH là cạnh góc vuông của và
\(\widehat {ABH} = \widehat {CBH}\)( Do cùng bằng \({90^o} - \widehat {HAB} = {90^o} - \widehat {HCB}\) )
\( \Rightarrow \) \(\Delta AHB = \Delta CHB\)
\( \Rightarrow \) BA = BC
(Trả lời bởi Hà Quang Minh)
Tìm các tam giác cân trong Hình 11 và đánh dấu vào các cạnh bằng nhau.
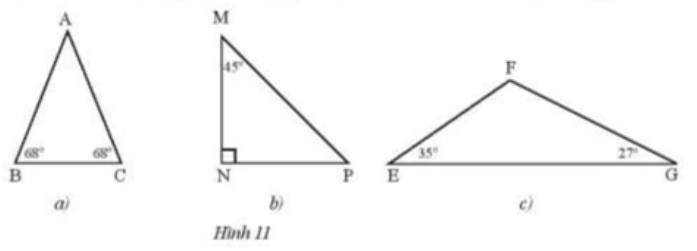
Thảo luận (1)Hướng dẫn giảia) Ta có tam giác ABC cân tại A do 2 góc đáy B, C cùng bằng 68°
Nên AB = AC
b) Vì tổng các góc trong tam giác = 180° nên \(\widehat M + \widehat N + \widehat P = {180^o}\)
\( \Rightarrow \widehat P = {180^o} - {45^o} - {90^o} = {45^o}\)
\( \Rightarrow \) \(\Delta MNP\) vuông cân tại N
\( \Rightarrow \) MN = NP
c) Xét \(\Delta EFG\) theo định lí về tổng số đo các góc trong tam giác ta có :
\( \Rightarrow \widehat F + \widehat E + \widehat G = {180^o}\)
\( \Rightarrow \widehat F = {180^o} - {35^o} - {27^o} = {118^o}\)
\( \Rightarrow \Delta EFG\) không cân nên không có các cặp cạnh bằng nhau
(Trả lời bởi Hà Quang Minh)
Cho tam giác ABC cân tại A có góc B bằng \({60^o}\). Chứng minh rằng tam giác ABC đều.
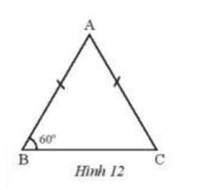
Thảo luận (1)Hướng dẫn giảiTa có: tam giác ABC cân tại A
Nên \(\widehat B = \widehat C = {60^o}\)( 2 góc đáy của tam giác cân )
Theo định lí về tổng 3 góc trong tam giác ta có : \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat A = {180^o} - {60^o} - {60^o} = {60^o}\)
Vì \(\widehat A = \widehat B = \widehat C = {60^o}\)\( \Rightarrow \) tam giác ABC là tam giác đều
(Trả lời bởi Hà Quang Minh)
Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích.
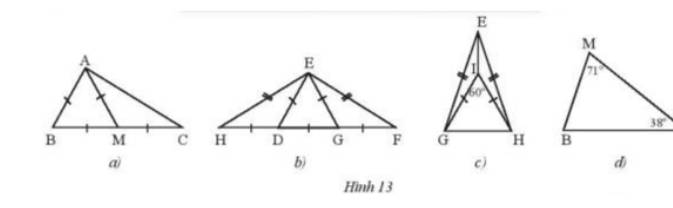
Thảo luận (1)Hướng dẫn giảia) Tam giác ABM là tam giác đều do có 3 cạnh bằng nhau
Tam giác AMC cân tại M do AM = MC
b) Tam giác EDG là tam giác đều do có 3 cạnh bằng nhau
Tam giác EHF cân tại E do EH = EF
Tam giác EDH cân tại D do DH = DE
c) Tam giác EGF cân tại G do GE = GF
Tam giác IHG đều do là tam giác cân có 1 góc = 60°
Tam giác EHG cân tại E do EG = EH
d) Tam giác MBC không cân và không đều vì 3 góc có số đo khác nhau.
(Trả lời bởi Hà Quang Minh)