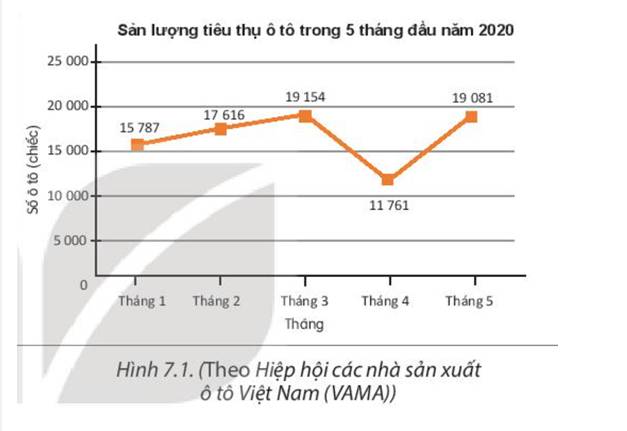
a) Tháng 4 số lượng ô tô tiêu thụ thấp nhất. Số lượng tiêu thụ trong tháng đó là 11 761 chiếc
b) y là một hàm số của x. x=5 => y=19081
Đúng 0
Bình luận (0)
Bài 27. Khái niệm hàm số và đồ thị của hàm số
Các câu hỏi tương tự
Hình 7.1 là biểu đồ đoạn thẳng mô tả sản phẩm tiêu thụ ô tô của thị trường Việt Nam trong 5 tháng đầu năm 2020. Em hãy cho biết trong tháng nào thì số lượng ô tô tiêu thụ là ít nhất.
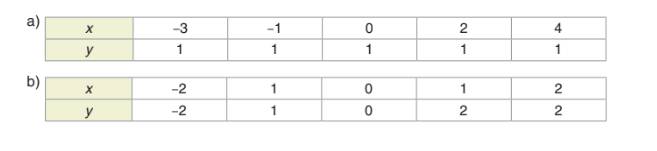
Các giá trị tương ứng của hai đại lượng x và y cho bởi các bảng sau. Đại lượng y có phải là một hàm số của x không?
Hình 7.10 là đồ thị của hàm số mô tả nhiệt độ T (°C) tại các thời điểm t (giờ) của một thành phố ở châu Âu từ giữa trưa đến 6 giờ tối a) Tìm T(1), T(2), T(5) và giải thích ý nghĩa các con số nàyb) Trong hai giá trị T(1) và T(4), giá trị nào lớn hơn c) Tìm t sao cho T (t) 5d) Trong khoảng thời gian nào thì nhiệt độ cao hơn 5 °C
Đọc tiếp
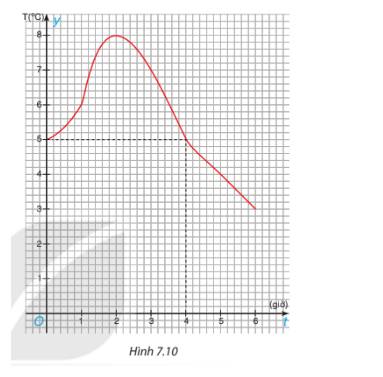
Hình 7.10 là đồ thị của hàm số mô tả nhiệt độ T (°C) tại các thời điểm t (giờ) của một thành phố ở châu Âu từ giữa trưa đến 6 giờ tối
a) Tìm T(1), T(2), T(5) và giải thích ý nghĩa các con số này
b) Trong hai giá trị T(1) và T(4), giá trị nào lớn hơn
c) Tìm t sao cho T (t) = 5
d) Trong khoảng thời gian nào thì nhiệt độ cao hơn 5 °C
Quãng đường đi được S (km) của một ô tô chuyển động với vận tốc 60km/h được cho bởi công thức S=60t, trong đó t(giờ) là thời gian ô tô di chuyển
a) Tính và lập bảng các giá trị tương ứng của S khi t nhận các giá trị lần lượt là 1; 2; 3; 4 (giờ)
b) Với mỗi giá trị của t, ta xác định được bao nhiêu giá trị tương ứng của S?
Cho hàm số: \(y=f\left( x \right)=\frac{4}{x}\)
a) Tính f(-4); f(8)
b) Hoàn thành bảng sau vào vở
Hàm số yf(x) được cho bởi bảng sau: x-2-1012y f(x)-10123a) Viết tập hợp {(x; y)} các cặp giá trị tương ứng của x và yb) Vẽ hệ trục tọa độ Oxy và biểu diễn các điểm có tọa độ là các cặp số trên. Tập hợp các điểm này gọi là đồ thị của hàm số y f(x) đã cho.
Đọc tiếp
Hàm số y=f(x) được cho bởi bảng sau:
x | -2 | -1 | 0 | 1 | 2 |
y= f(x) | -1 | 0 | 1 | 2 | 3 |
a) Viết tập hợp {(x; y)} các cặp giá trị tương ứng của x và y
b) Vẽ hệ trục tọa độ Oxy và biểu diễn các điểm có tọa độ là các cặp số trên. Tập hợp các điểm này gọi là đồ thị của hàm số y= f(x) đã cho.
Viết công thức tính thời gian di chuyển trên quãng đường dài 150 km với vận tốc không đổi v (km/h). Thời gian di chuyển t có phải là một hàm số của vận tốc v không? Tính giá trị của t khi v=60 (km/h)
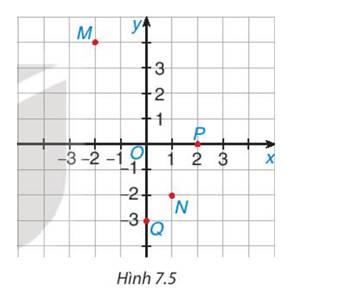
a) Xác định tọa độ của các điểm M,N,P,Q trong Hình 7.5
b) Xác định các điểm R(2; -2) và S(-1; 2) trong Hình 7.5
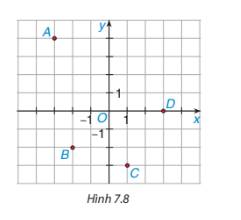
a) Xác định tọa độ của các điểm A, B, C, D trong Hình 7.8
b) Xác định các điểm E (0;-2) và F (2;-1) trong Hình 7.8
