Chương 1: VECTƠ
Các câu hỏi tương tự
Bài 1: Cho đường tròn (I; R) nội tiếp tam giác ABC tiếp xúc với BC tại D. Gọi M và N lần lượt là trung điểm của AD và BC. Chứng minh M, I, N thẳng hàng Bài 2: cho đường tròn tâm O và 3 dây cung song song với nhau là AA, BB, CC. Chứng minh rằng trực tâm các tam giác ABC; BCA và CAB cùng nằm trên 1 đường thẳng Bài 3: Trên đường thẳng a cho các điểm A, B, C và trên đường thẳng b cho M, N, P thỏa mãn vectoABk. vectoAC và vectoMNk. vectoMP (k khác 1). Giả sử X, Y, Z là các điểm chia các đoạn thẳng AM...
Đọc tiếp
Bài 1: Cho đường tròn (I; R) nội tiếp tam giác ABC tiếp xúc với BC tại D. Gọi M và N lần lượt là trung điểm của AD và BC. Chứng minh M, I, N thẳng hàng
Bài 2: cho đường tròn tâm O và 3 dây cung song song với nhau là AA', BB', CC'. Chứng minh rằng trực tâm các tam giác ABC'; BCA' và CAB' cùng nằm trên 1 đường thẳng
Bài 3: Trên đường thẳng a cho các điểm A, B, C và trên đường thẳng b cho M, N, P thỏa mãn vectoAB=k. vectoAC và vectoMN=k. vectoMP (k khác 1). Giả sử X, Y, Z là các điểm chia các đoạn thẳng AM, BN và CP theo cùng 1 tỉ số. CMR: X, Y, Z thẳng hàng
Bài 4: Cho góc xOy và 2 điểm M, N di chuyển trên 2 cạnh Ox, Oy thỏa mãn OM=2ON.
a)) CMR: trung điểm I của MN luôn thuộc 1 đường thẳng cố định
b)) Nghiên cứu trường hợp giả thiết thay OM=2ON thành OM=mON với m là 1 hằng số cố định
c)) Nghiên cứu trường hợp thay giả thiết I là trung điểm MN thành giả thiết I là điểm chia MN theo tỉ số k cố định. (toán lớp 10 ạ)
Cho tam giác ABC. Gọi M, N, I lần lượt là các điểm thảo mãn 2AM+2BM=2IA+3IB-IC=0
1) Phân tích vecto AM, AI theo AB, AC
2) Chứng minh: 3 điểm C, N, I thẳng hàng
Bài 1:Cho điểm I thuộc đoạn thẳng AB, I khác A và B. Chứng minh rằng overrightarrow{OI}frac{IB}{IA}overrightarrow{OA}+frac{IA}{AB}overrightarrow{OB}forall OBài 2:Cho tam giác ABC, các điểm M,N,P thỏa mãn overrightarrow{BM}frac{-1}{3}overrightarrow{BC},overrightarrow{AN}frac{2}{5}overrightarrow{AC},overrightarrow{AP}xoverrightarrow{AB}.Tìm x biết rằng M,N,P thẳng hàng.Ai giúp mình với chiều mai kiểm tra 2 bài này rồi mà mình nháp mãi chẳng ra.... :
Đọc tiếp
Bài 1:
Cho điểm I thuộc đoạn thẳng AB, I khác A và B. Chứng minh rằng \(\overrightarrow{OI}=\frac{IB}{IA}\overrightarrow{OA}+\frac{IA}{AB}\overrightarrow{OB}\forall O\)
Bài 2:
Cho tam giác ABC, các điểm M,N,P thỏa mãn \(\overrightarrow{BM}=\frac{-1}{3}\overrightarrow{BC},\overrightarrow{AN}=\frac{2}{5}\overrightarrow{AC},\overrightarrow{AP}=x\overrightarrow{AB}.\)Tìm x biết rằng M,N,P thẳng hàng.
Ai giúp mình với chiều mai kiểm tra 2 bài này rồi mà mình nháp mãi chẳng ra.... :<
cho tam giác ABC có trọng tâm G và 2 điểm M,N sao cho : vecto 3MA+ 4MB = 0 và veco NB-3NC=0 . Chứng minh 3 điểm M, N , G thẳng hàng
Mọi người giúp mình làm với cảm ơn nhìu ạ
Cho Δ ABC . Trên tia BC lấy điểm D sao cho 3BD 2BC (3 lần vecto BD 2 lần vecto BC ) . Gọi E là điểm thỏa mãn : 3EA+EB+2EC 0 (vecto) a. Biểu thị vecto AD , AE theo 2 vecto AB , ACb. Chứng minh A , E , D thẳng hàng và E là trung điểm ADc. Trên AC lấy F và đặt FA kAC (k ϵ R , vecto) . Tìm k để B , E , F thẳng hàng
Đọc tiếp
Cho Δ ABC . Trên tia BC lấy điểm D sao cho 3BD = 2BC (3 lần vecto BD = 2 lần vecto BC ) . Gọi E là điểm thỏa mãn : 3EA+EB+2EC = 0 (vecto)
a. Biểu thị vecto AD , AE theo 2 vecto AB , AC
b. Chứng minh A , E , D thẳng hàng và E là trung điểm AD
c. Trên AC lấy F và đặt FA = kAC (k ϵ R , vecto) . Tìm k để B , E , F thẳng hàng
Cho △ABC có trọng tâm G và 2 điểm M, N sao cho: AB 3AM; CD 2CN a) Chứng minh: 3 điểm M, N, G thẳng hàng b) Biểu diễn overrightarrow{AC} qua 2 vecto overrightarrow{AG} và overrightarrow{AN} c) Gọi k là giao điểm của AC và GN. Tính tỉ số dfrac{KA}{KB}
Đọc tiếp
Cho △ABC có trọng tâm G và 2 điểm M, N sao cho: AB = 3AM; CD = 2CN
a) Chứng minh: 3 điểm M, N, G thẳng hàng
b) Biểu diễn \(\overrightarrow{AC}\) qua 2 vecto \(\overrightarrow{AG}\) và \(\overrightarrow{AN}\)
c) Gọi k là giao điểm của AC và GN. Tính tỉ số \(\dfrac{KA}{KB}\)
Đề là chứng minh M N và P thẳng hàng nha cái chỗ khó nhìn là thoả mãn
Giúp mik với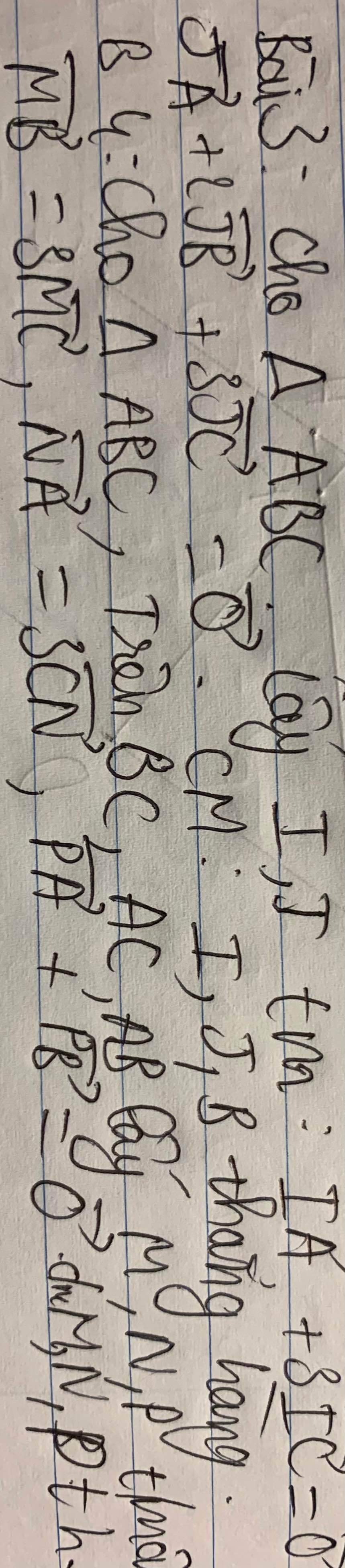
Cho tam giác ABC. Trên các đường thẳng BC, AC, AB lần lượt lấy các điểm M, N, P sao cho overrightarrow{NA}3.overrightarrow{CN}; overrightarrow{MB}3.overrightarrow{MC}; overrightarrow{PA}+overrightarrow{PB}overrightarrow{0} a) Tính overrightarrow{PM}; overrightarrow{PN} theo overrightarrow{AB};overrightarrow{AC} b) Chứng minh: M, N, P thẳng hàng
Đọc tiếp
Cho tam giác ABC. Trên các đường thẳng BC, AC, AB lần lượt lấy các điểm M, N, P sao cho \(\overrightarrow{NA}=3.\overrightarrow{CN}\); \(\overrightarrow{MB}=3.\overrightarrow{MC}\); \(\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}\)
a) Tính \(\overrightarrow{PM}\); \(\overrightarrow{PN}\) theo \(\overrightarrow{AB};\overrightarrow{AC}\)
b) Chứng minh: M, N, P thẳng hàng
cho tam giác ABC trung tuyến AD. Gọi M là trung điểm AD, xét N ch bởi véc tơ AC bằng 3 lần véc tơ AN . CMR : B , M , N thẳng hàng










