Xét ΔABC có P,Q lần lượt là trung điểm của AB,AC
=>PQ là đường trung bình
=>PQ=BC/2=4,5(cm)
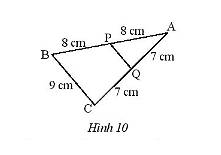
Vì \(PA = 8cm;PB = 8cm \Rightarrow PA = PB \Rightarrow P\) là trung điểm của \(AB\).
Vì \(CQ = 7cm;AQ = 7cm \Rightarrow CQ = AQ \Rightarrow Q\) là trung điểm của \(AC\).
Xét tam giác \(ABC\) có:
\(P\) là trung điểm của \(AB\); \(Q\) là trung điểm của \(AC\) nên \(PQ\) là đường trung bình của tam giác \(ABC\).
\( \Rightarrow PQ = \frac{1}{2}BC\) (tính chất đường trung bình)
\( \Leftrightarrow PQ = \frac{1}{2}.9 = 4,5cm\).
Vậy \(PQ = 4,5cm\).