Bài 3: Hình thang cân
Các câu hỏi tương tự
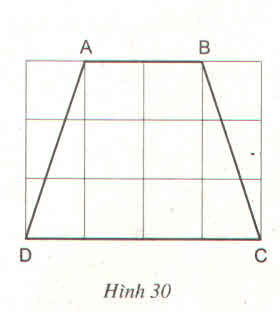
Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (H.30, độ dài của cạnh ô vuông là 1cm)
hình thang cân abcd ab//cd) đáy lớn = 2,7cm .cạnh bên dài 1cm, góc adc=60 độ . kẻ ae//bc. tính độ dài ab
giúp mk với
Một hình thang cân có đường chéo vuông góc với cạnh bên, cạnh bên và đáy nhỏ cùng bằng 1cm. Tính độ dài đáy lớn và đường chéo của hình thang đó
Đố :
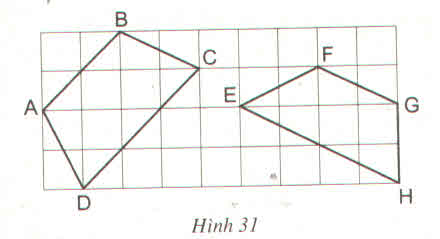
Trong các tứ giác ABCD và EFGH trên giấy kẻ ô vuông (h.31) tứ giác nào là hình thang cân ? Vì sao ?
Bài 1: Cho hình thang cân ABCD (AB//CD) có AB3,BCCD13(cm). Kẻ các đường cao AK và BH.a) Chứng minh rằng CHDK.b) Tính độ dài BH.Bài 2: Hình thang cân ABCD (AB//CD) có Cˆ600, DB là tia phân giác của góc D, AB4cm.a) Chứng minh rằng BD vuông góc với BC.b) Tính chu vi hình thang.Bài 3: Cho hình thang cân ABCD (AB//CD, AB CD). AD cắt BC tại O.a) Chứng minh rằng ΔOAB cân.b) Gọi I, J lần lượt là trung điểm của AB và CD. Chứng minh rằng ba điểm I, J, O thẳng hàng.c) Qua điểm M thuộc cạnh AC, vẽ đường th...
Đọc tiếp
Bài 1: Cho hình thang cân ABCD (AB//CD) có AB=3,BC=CD=13(cm). Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Tính độ dài BH.
Bài 2: Hình thang cân ABCD (AB//CD) có Cˆ=600, DB là tia phân giác của góc D, AB=4cm.
a) Chứng minh rằng BD vuông góc với BC.
b) Tính chu vi hình thang.
Bài 3: Cho hình thang cân ABCD (AB//CD, AB < CD). AD cắt BC tại O.
a) Chứng minh rằng ΔOAB cân.
b) Gọi I, J lần lượt là trung điểm của AB và CD. Chứng minh rằng ba điểm I, J, O thẳng hàng.
c) Qua điểm M thuộc cạnh AC, vẽ đường thẳng song song với CD, cắt BD tại N. Chứng minh rằng MNAB, MNDC là các hình thang cân.
Bài 1: Cho hình thang cân ABCD (AB//CD) có AB3,BCCD13(cm). Kẻ các đường cao AK và BH.a) Chứng minh rằng CHDK.b) Tính độ dài BH.Bài 2: Hình thang cân ABCD (AB//CD) có Cˆ600, DB là tia phân giác của góc D, AB4cm.a) Chứng minh rằng BD vuông góc với BC.b) Tính chu vi hình thang.Bài 3: Cho hình thang cân ABCD (AB//CD, AB CD). AD cắt BC tại O.a) Chứng minh rằng ΔOAB cân.b) Gọi I, J lần lượt là trung điểm của AB và CD. Chứng minh rằng ba điểm I, J, O thẳng hàng.c) Qua điểm M thuộc cạnh AC, vẽ đường th...
Đọc tiếp
Bài 1: Cho hình thang cân ABCD (AB//CD) có AB=3,BC=CD=13(cm). Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Tính độ dài BH.
Bài 2: Hình thang cân ABCD (AB//CD) có Cˆ=600, DB là tia phân giác của góc D, AB=4cm.
a) Chứng minh rằng BD vuông góc với BC.
b) Tính chu vi hình thang.
Bài 3: Cho hình thang cân ABCD (AB//CD, AB < CD). AD cắt BC tại O.
a) Chứng minh rằng ΔOAB cân.
b) Gọi I, J lần lượt là trung điểm của AB và CD. Chứng minh rằng ba điểm I, J, O thẳng hàng.
c) Qua điểm M thuộc cạnh AC, vẽ đường thẳng song song với CD, cắt BD tại N. Chứng minh rằng MNAB, MNDC là các hình thang cân.
Cho hình thang cân ABCD (AB // CD, AB < CD), biết AC vuông góc với BD . Gọi M, N lần lượt là trung điểm của AD và BC. Kẻ AH vuông góc với CD (H thuộc CD) biết AH=10cm . Khi đó, độ dài MN là
A.9cm B.10cm C.6cm D.8cm
1. Cho hình thang cân ABCD có AB || CD, AB 3 cm, CD6 cm, AD2,5 cm. Gọi M, N lần lượt là hình chiếu của A, B trên đường thẳng CD. Tính độ dài các đoạn thẳng DM, DN, AM.2. Cho tam giác ABC cân tại A. Lấy điểm M, N lần lượt trên cạnh AB, AC sao choAM AN.a) Chứng minh tứ giác BMNC là hình thang cân.b) Xác định vị trí các điểm M, N để BMMNNC.3. Cho tứ giác ABCD có C D và AD BC. Chứng minh tứ giác ABCD là hình thang cân.
Đọc tiếp
1. Cho hình thang cân ABCD có AB || CD, AB= 3 cm, CD=6 cm, AD=2,5 cm. Gọi M, N lần lượt là hình chiếu của A, B trên đường thẳng CD. Tính độ dài các đoạn thẳng DM, DN, AM.
2. Cho tam giác ABC cân tại A. Lấy điểm M, N lần lượt trên cạnh AB, AC sao cho
AM = AN.
a) Chứng minh tứ giác BMNC là hình thang cân.
b) Xác định vị trí các điểm M, N để BM=MN=NC.
3. Cho tứ giác ABCD có C = D và AD = BC. Chứng minh tứ giác ABCD là hình thang cân.
Đố :
Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32).
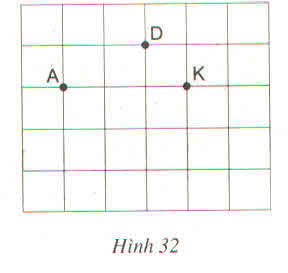
Hãy tìm điểm thứ tư M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình thang cân.







