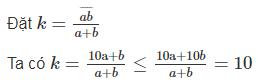Question

Tìm số tự nhiên có hai chữ số sao cho tỉ số đó với tổng các chữ số của nó là lớn nhất ?

Answer 1

Gọi tỉ số giữa \(\overline{ab}\) và a + b là k, ta có:

k = \(\dfrac{\overline{ab}}{a+b}=\dfrac{10a+b}{a+b}=1+\dfrac{9a}{a+b}=1+\dfrac{9}{1+\dfrac{b}{a}}\)

Để k lớn nhất thì \(\dfrac{9}{1+\dfrac{b}{a}}\) lớn nhất => \(1+\dfrac{b}{a}\) nhỏ nhất => \(\dfrac{b}{a}\) nhỏ nhất => b = 0 và a là số tự nhiên bất kì từ 1 đến 9

Answer 2

k = 10 ⇔ b = 10b ⇔ b = 0

Như vậy k lớn nhất bằng 10 ứng với các số 10; 20; 30; …; 90.

Answer 3

k = 10 ⇔ b = 10b ⇔ b = 0

Như vậy k lớn nhất bằng 10 ứng với các số 10; 20; 30; …; 90.