\(\sqrt{x^2-4x+4}\)
\(=\sqrt{x^2-2\cdot2\cdot x+2^2}\)
\(\sqrt{\left(x-2\right)^2}\)
Xác định khi \(\left(x-2\right)^2\ge0\) (luôn đúng)
Vậy biểu thức được xác định với mọi x
\(\sqrt{x^2-4x+4}\)
\(=\sqrt{x^2-2\cdot2\cdot x+2^2}\)
\(\sqrt{\left(x-2\right)^2}\)
Xác định khi \(\left(x-2\right)^2\ge0\) (luôn đúng)
Vậy biểu thức được xác định với mọi x
Bài 1 Cho 2 biểu thức A=\(\sqrt{50}-3\sqrt{8}+\sqrt{\left(\sqrt{2}-1\right)^2}\)và B=\(\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}\) (\(Đk:x\ge0;x\ne1\))
a) Rút gọn A,B
b)Tìm giá trị của x để giá trị biểu thức A bằng giá trị biểu thức B
giải phương trình
a) \(\sqrt{x-5}\)+\(\sqrt{4x-20}\)-\(\dfrac{1}{5}\)\(\sqrt{9x-45}\)=3
b) \(\sqrt{x-1}\)+\(\sqrt{4x-4}\)-\(\sqrt{25x-25}\)+2=0
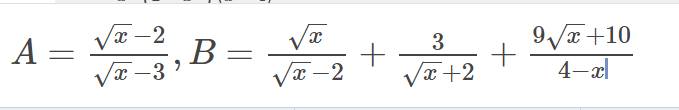
a,tính giá trị biểu thức A khi x=16/9
b,rút gọn biểu thức B
c,cho P=B/A,Tìm các giá trị của x là số thực đẻ P nhận giá trị nguyên
1. Rút gọn
A=\(\sqrt{2}\left(\sqrt{8}-3\right)+\sqrt{18}\)
2.
a) Cho hàm số y=ax-3, biết đồ thị hàm số đi qua điểm A(-3:18). Tìm a và xác định công thức hàm số.
b) Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình: y=(m+1)x-n. Viết phương trình của d, biết d đi qua điểm A(1:-1) và có hệ số góc bằng -3
1.1
a. \(\sqrt{12}\)-\(\sqrt{27}\)+\(\sqrt{4+2\sqrt{3}}\)
b. (\(\dfrac{\sqrt{a}}{2+\sqrt{a}}\) +\(\dfrac{4+a}{4-a}\) ).(2\(\sqrt{a}\) -a) với a ≥ 0, a ≠4
1.2 giải hệ phương trình \(\left\{{}\begin{matrix}3x-y=5\\2y-x=10\end{matrix}\right.\)
2. Rút gọn phương trình.
a) \(M=\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\)
b) \(P=(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2}{x-\sqrt{x}}):\dfrac{1}{\sqrt{x}-1}\) với x >0, x ≠1
3. a) giải hệ phương trình \(\left\{{}\begin{matrix}4x-3y=2\\3y+4x=-18\end{matrix}\right.\)
b) \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}+4}+\dfrac{4}{\sqrt{x}-4}\right)\dfrac{x+16}{\sqrt{x}+2}\) với x ≥0, x≠16
4. Tìm m để đường thẳng y=(2m-1)x+3 song song với đường thẳng y=5x-1
Cho pt x^2-mx-1=0 a) chứng minh pt có 2 nghiệm trái dấu b) gọi x1,x2 là các nghiệm của pt 1 Tính giá trị của biểu thức P= x1^2+x1-1/x1 - x2^2+x2-1/x2
Cho x và y là hai số thực dương thỏa mãn 3x+y ≤4
Tìm giá trị nhỏ nhất của biểu thức A=1/x + 1/√(xy)
Quy tắc sau đây cho ta biết CAN, CHI của năm X nào đó. Để xác định CAN, ta tìm số dư r trong phép chia X cho 10 và tra vào bảng 1. r 0 1 2 3 4 5 6 7 8 9 CAN Canh Tân Nhâm Quý Giáp Ất Bính Đinh Mậu Kỷ Để xác định CHI, ta tìm số dư s trong phép chia X cho 12 và tra vào bảng 2. s 0 1 2 3 4 5 6 7 8 9 10 11 CHI Thân Dậu Tuất Hợi Tí Sửu Dần Mẹo Thìn Tỵ Ngọ Mùi Ví dụ: năm 2020 có CAN là Canh, CHI là Tí. a. Em hãy sữ dụng quy tắc trên để xác định CAN, CHI của năm 2023? b. Lý Thái Tổ ( Lý Công Uẩn) là vị vua đầu tiên đã mở nên triều đại Lý Phồn Thịnh trong suốt hơn 200 năm. Ông lên ngôi vào năm Kỷ Dậu đầu thế kỉ 11. Em hãy cho biết ông lên ngôi vào năm nào ?
Đặt cho 3^x=7^y=441, hãy tìm giá trị của (xy/x+y)^2