Đề số 1
Các câu hỏi tương tự
Bài 1 Cho 2 biểu thức A=\(\sqrt{50}-3\sqrt{8}+\sqrt{\left(\sqrt{2}-1\right)^2}\)và B=\(\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}\) (\(Đk:x\ge0;x\ne1\))
a) Rút gọn A,B
b)Tìm giá trị của x để giá trị biểu thức A bằng giá trị biểu thức B
giải phương trình: x2 - 2x = 2√2x-1
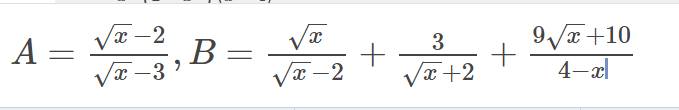
a,tính giá trị biểu thức A khi x=16/9
b,rút gọn biểu thức B
c,cho P=B/A,Tìm các giá trị của x là số thực đẻ P nhận giá trị nguyên
Cho x và y là hai số thực dương thỏa mãn 3x+y ≤4
Tìm giá trị nhỏ nhất của biểu thức A=1/x + 1/√(xy)
Bài 2.2 Giá trị của một chiếc máy tính bảng sau khi sử dụng t năm được cho bởi công thức
V(t)=9800000-1200000*t (đồng)
a)Hãy tính V(2) và cho biết V(2) có nghĩa là gì ?
b)Sau bao nhiêu năm thì giá trị của chiếc máy tính bảng là 5000000 đồng
2.Cho tam giác ABC vuông tại A, đường cao AH . Biết AB = 6cm AC = 8cm . a) Tính BC; BH và số đo góc C (số đo góc làm tròn đến độ) b) Gọi E, F là hình chiếu của H trên AB, AC . Chứng minh AE.BE+AF. CF = A * H ^ 2 c) Gọi I là trung điểm của BC, AI cắt EF tại O. Chứng minh: 1/(O * A ^ 2) = 1/(A * E ^ 2) + 1/(A * F ^ 2)
cho tam giác ABCD vuông tại A biết AB = 6 cm AC bằng 8 cm 1. Giải tam giác vuông ABCD (số đo góc làm tròn đến độ) 2. Từ A kẻ AK vuông góc với BC ( K thuộc BC ). gọi E, F lần lượt là hình chiếu của K trên AB và AC, EF cắt AK tại i. chứng minh BK.KC = 4 EI . IF
Cho ∆MAB có 3 góc nhọn. Vẽ đường tròn tâm O đường kính AB cắt MA và MB lần lượt tại D và C. Gọi H là giao điểm của AC và BD. a) Chứng minh: ∆ ABC vuông và MH AB b) Gọi P, N, Q theo thứ tự là chân các đường vuông góc kẻ từ A, O, B đến CD. Chứng minh: PD = CQ c) Gọi I là trung điểm của MH. Chứng minh: IC là tiếp tuyến của (O)
Giải nhanh giúp e với ạ
1. Rút gọn
A=\(\sqrt{2}\left(\sqrt{8}-3\right)+\sqrt{18}\)
2.
a) Cho hàm số y=ax-3, biết đồ thị hàm số đi qua điểm A(-3:18). Tìm a và xác định công thức hàm số.
b) Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình: y=(m+1)x-n. Viết phương trình của d, biết d đi qua điểm A(1:-1) và có hệ số góc bằng -3













