Ta có \(\widehat{A}>\widehat{B}>\widehat{C}\) nên \(BC>AC>AB\)
Do đó \(OH< OI< OK\)
Đúng 0
Bình luận (0)
Bài 3: Liên hệ giữa dây và khoảng cách từ tâm tới dây
Các câu hỏi tương tự
Cho tam giác MNP nội tiếp (O) có góc M< góc N< góc P. Gọi OH, OK, OI lần lượt là khoảng cách từ O đến MN, NP, MP. So sánh OH, OK, OI
Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.
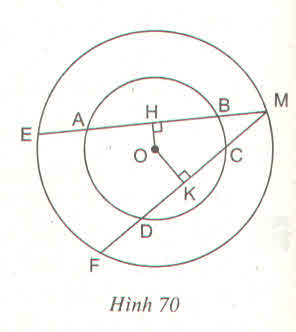
Hãy so sánh các độ dài :
a) OH và OK
b) ME và MF
c) MH và MK
Cho đường tròn (O), có dây AB và dây CD bằng nhau và không cắt nhau. Gọi M là giao điểm của các tia AB, CD. Gọi I,K lần lượt là trung điểm của AB, CD. CMR:
a) IK \(\perp\) MO, IK // AC.
b) Tính bán kính đường tròn (O) nếu OI = 4cm, \(\widehat{AMC}=40^0\), \(\widehat{AIK}=2\widehat{AIC}\)
đường tròn tâm O bán kính r dây AB=24, AC=20 M là trung điểm của AC khoảng cách từ M tới AB là MH=8, Kẻ OK vuông góc với AB
a) C,O,K thẳng hàng
b) Tính R
1,Cho tam giác abc nội tiếp đường tròn o, biết b=60, c=40. Hãy sắp xếp thứ tự các khoảng cách từ tâm o đến cạnh ab,ac ,bc.
2, cho đường tròn tâm o bán kính 5cm . Vẽ dây ab sao cho khoảng cách từ O đến ab=4 . Tính ab
3 cho đường tròn tâm O bán kính ab , dây cd không cắt ab . Qua c, d vẽ các đường thẳng vuông góc với cd, ab thứ tự tại k, h . Chứng minh AH=BK
Cho đường tròn tâm O, đường kính AB = 13cm. Dây CD có độ dài bằng 12cm và vuông
góc với AB tại H. Gọi M, N theo thứ tự là hình chiếu của H trên AC, BC. Tính diện tích tứ giác
CMHN.
Cho góc xOy khác góc bẹt, hai cạnh Ox, Oy cắt đường tròn tâm M theo hai dây AB và CD sao cho AB > CD Vẽ MH perp AB tại H, MK I CD tại K. So sánh OH với OK.
Cho(O,R), dây AB=24cm, AC=20cm ( góc BAC<90o và điểm O nằm trong góc BAC). Gọi M là trung điểm của AC. Khoảng cách từ M đến AB bằng 8cm
a) C/m: tam giác ABC cân tại C
b) Tính R
Cho đường tròn tâm O,2 dây AB,CD bằng nhau E là giao điểm AB,CD.Gọi I và K theo thứ tự là chân đường vuông góc kẻ từ O đến AB,CD.CMR
a,tam giác EIO=tam giác EKO
b,EO là đường trung trực IK
c,tam giac AEC cân tại E