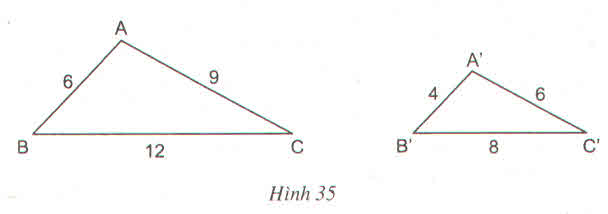
Do ΔABC ∼ ΔA'B'C' nên:
\(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
⇔ \(\frac{A'B'}{3}=\frac{B'C'}{7}=\frac{C'A'}{5}\)
= \(\frac{A'B'+B'C'+C'A'}{3+7+5}=\frac{55}{15}=\frac{11}{3}\) (tính chất dãy tỉ số bằng nhau)
\(\Leftrightarrow\left\{{}\begin{matrix}A'B'=\frac{11}{3}.3=11\\B'C'=\frac{11}{3}.7=\frac{77}{3}\\C'A'=\frac{11}{3}.5=\frac{55}{3}\end{matrix}\right.\)
Vậy A'B' = 11cm; B'C' = \(\frac{77}{3}cm\); C'A' = \(\frac{55}{3}cm\)