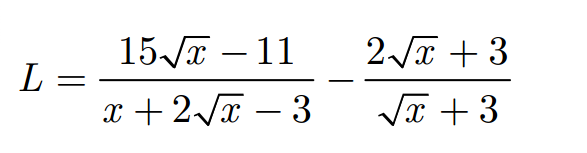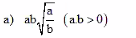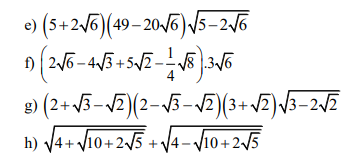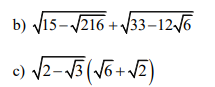\(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}-\dfrac{6\sqrt{x}-4}{x-1}\)
\(ĐKXĐ:x\ge0,x\ne1\)
\(\Leftrightarrow\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)+3\left(\sqrt{x}-1\right)-6\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x-1}\right)}\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
Vậy kết quả rút gọn của P là \(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)