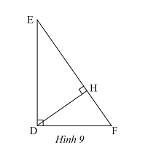
a) Xét \(\Delta DEF\) và \(\Delta HDF\) có:
\(\widehat F\) chung
\(\widehat {EDF} = \widehat {DHF} = 90^\circ \)
Do đó, \(\Delta DEF\backsim\Delta HDF\) (g.g)
b) Vì \(\Delta DEF\backsim\Delta HDF\) nên \(\frac{{DF}}{{HF}} = \frac{{FE}}{{DF}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
\( \Rightarrow D{F^2} = FH.FE\).
c) Theo câu b ta có:
\(D{F^2} = FH.FE\)
Thay số, \(D{F^2} = 5,4.15 = 81 \Rightarrow DF = \sqrt {81} = 9cm\)
Vậy \(DF = 9cm\).