Question

Cho hai tam giác vuông \(ABC\) và \(DEF\) có các kích thước như Hình 4.

a) Hãy tính độ dài cạnh \(AC\) và \(DF\).

b) So sánh các tỉ số \(\frac{{AB}}{{DE}};\frac{{AC}}{{DF}}\) và \(\frac{{BC}}{{EF}}\).

c) Dự đoán sự đồng dạng của hai tam giác\(ABC\) và \(DEF\).

Answer 1

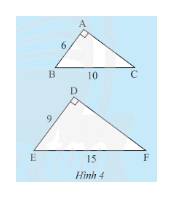
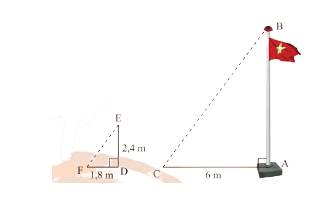
a) Xét tam giác \(ABC\) vuông tại \(A\) ta có:

\(A{B^2} + A{C^2} = B{C^2}\) (định lí Py – ta – go)

\( \Leftrightarrow {6^2} + A{C^2} = {10^2} \Leftrightarrow A{C^2} = {10^2} - {6^2} = 64 \Leftrightarrow AC = 8\).

Xét tam giác \(DEF\) vuông tại \(D\) ta có:

\(D{E^2} + D{F^2} = E{F^2}\) (định lí Py – ta – go)

\( \Leftrightarrow {9^2} + D{F^2} = {15^2} \Leftrightarrow D{F^2} = {15^2} - {9^2} = 144 \Leftrightarrow DF = 12\).

b) Tỉ số:

\(\frac{{AB}}{{DE}} = \frac{6}{9} = \frac{2}{3};\frac{{AC}}{{DF}} = \frac{8}{{12}} = \frac{2}{3}\); \(\frac{{BC}}{{EF}} = \frac{{10}}{{15}} = \frac{2}{3}\).

Do đó, \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\).

c) Xét tam giác\(ABC\) và tam giác\(DEF\) có:

\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}\) (chứng minh trên)

Do đó, \(\Delta ABC\backsim\Delta DEF\) (c.c.c)