\(\left(P\right)\perp\left(R\right);\left(Q\right)\perp\left(R\right)\)
Nền nhà, cánh cửa và mép cánh cửa ở Hình 48 gợi nên hình ảnh mặt mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) và đường thẳng \(a\) nằm trên mặt phẳng \(\left( P \right)\). Quan sát Hình 48 và cho biết:
a) Vị trí tương đối của đường thẳng \(a\) và mặt phẳng \(\left( Q \right)\);
b) Hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) có vuông góc với nhau không.
Hai vách ngăn tủ trong Hình 45 gợi nên hình ảnh hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau tạo nên bốn góc nhị diện. Các góc nhị diện đó có phải là những góc nhị diện vuông hay không?
Cho lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh cùng bằng \(a\), hai mặt phẳng \(\left( {A'AB} \right)\) và \(\left( {A'AC} \right)\) cùng vuông góc với \(\left( {ABC} \right)\).
a) Chứng minh rằng \(AA' \bot \left( {ABC} \right)\).
b) Tính số đo góc giữa đường thẳng \(A'B\) và mặt phẳng \(\left( {ABC} \right)\).
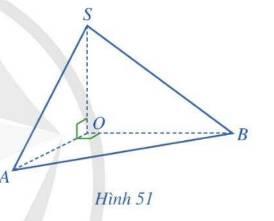
Cho hình chóp \(S.OAB\) thoả mãn \(\left( {AOS} \right) \bot \left( {AOB} \right)\), \(\widehat {AOS} = \widehat {AOB} = {90^ \circ }\) (Hình 51).
a) Giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) là đường thẳng nào?
b) \(SO\) có vuông góc với giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) hay không?
c) \(SO\) có vuông góc với mặt phẳng \(\left( {AOB} \right)\) hay không?
Chứng minh các định lí sau:
a) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai mặt phẳng đó thì vuông góc với mặt còn lại;
b) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó.
Chứng minh định lí sau: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
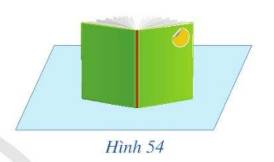
Trong Hình 54, hai bìa của cuốn sách gợi nên hình ảnh hai mặt phẳng vuông góc với mặt bàn. Hãy dự đoán xem gáy sách có vuông góc với mặt bàn hay không.
Cho một đường thẳng không vuông góc với mặt phẳng cho trước. Chứng minh rằng tồn tại duy nhất một mặt phẳng chứa đường thẳng đó và vuông góc với mặt phẳng đã cho.
Nêu ví dụ trong thực tiễn minh hoạ hình ảnh hai mặt phẳng vuông góc.
