\(2{x^2} - 4xy + 2y - x = \left( {2{x^2} - 4xy} \right) + \left( {2y - x} \right) = 2x\left( {x - 2y} \right) - \left( {x - 2y} \right) = \left( {x - 2y} \right)\left( {2x - 1} \right)\)
Bài 9. Phân tích đa thức thành nhân tử
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Phân tích các đa thức sau thành nhân tử:
\(\begin{array}{l}a)\,{x^2} - 6x + 9 - {y^2};\\b)\,4{x^2} - {y^2} + 4y - 4;\\c)\,xy + {z^2} + xz + yz;\\d)\,{x^2} - 4xy + 4{y^2} + xz - 2yz.\end{array}\)
Phân tích các đa thức sau thành nhân tử:
\(\begin{array}{l}a)\,{x^2} + xy;\\b)\,6{a^2}b - 18ab;\\c)\,{x^3} - 4x;\\d)\,{x^4} - 8x.\end{array}\)
Phân tích các đa thức sau thành nhân tử:
a) \({x^2} - 9 + xy + 3y\)
b) \({x^2}y + {x^2} + xy - 1\)
Phân tích các đa thức sau thành nhân tử
a) \({\left( {x + 1} \right)^2} - {y^2}\)
b) \({x^3} + 3{x^2} + 3x + 1\)
c) \(8{x^3} - 12{x^2} + 6x - 1\)
Hãy viết đa thức \({x^2} - 2xy\) thành tích của các đa thức, khác đa thức là số.
Tính nhanh giá trị của biểu thức
\(A = {x^2} + 2y - 2x - xy\) tại \(x = 2022,y = 2020\)
Phân tích đa thức \({x^3} - x\) thành nhân tử.
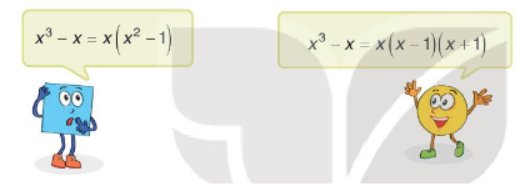
Em hãy nêu ý kiến của em về lời giải của Tròn và Vuông.
Phân tích các đa thức sau thành nhân tử:
a) \(6{y^3} + 2y\)
b) \(4\left( {x - y} \right) - 3x\left( {x - y} \right)\)
Giải bài toán mở đâu bằng cách phân tích \(2{x^2} + x\) thành nhân tử.



