Đáp án c và d vì: \({5^2} = {3^2} + {4^2}{;^{}}{\left( {2\sqrt 2 } \right)^2} = {2^2} + {2^2}\)
Bài 35. Định lí Pythagore và ứng dụng
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác vuông ABC có hai cạnh góc vuông AB=3cm,AC=4cm (H.9.31). Hãy đo độ dài cạnh BC và so sánh hai đại lượng \(A{B^2} + A{C^2}\) với \(B{C^2}\)
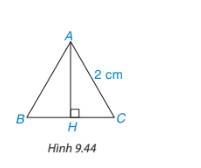
Tính chiều cao theo đơn vị centimét của một tam giác đều cạnh 2cm (h.9.44) (làm tròn kết quả đến chữ số thập phân thứ hai)
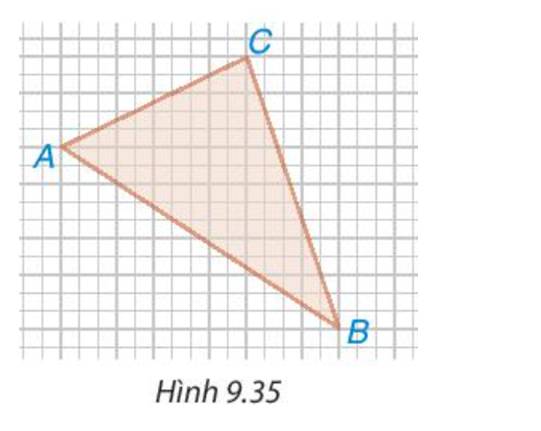
Trên giấy kẻ ô vuông (cạnh ô vuông bằng 1 cm), cho các điểm A, B, C như Hình 9.35. Tính độ dài các cạnh của tam giác ABC.
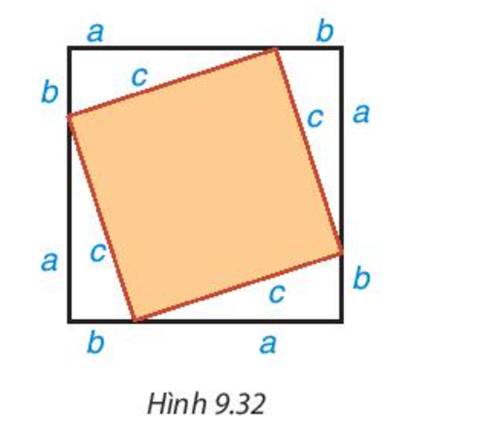
Lấy giấy trắng cắt bốn tam giác vuông bằng nhau. Gọi a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của các tam giác vuông này. Cắt một hình vuông bằng tấm bìa có cạnh dài a+b. Dán bốn tam giác vuông lên tấm bìa như Hình 9.32- Dùng ê ke kiểm tra phần bìa không bị che lấp có phải là hình vuông cạnh bằng c không. Từ đó tính diện tích phần bìa này theo c- Tổng diện tích bốn tam giác vuông có độ dài hai cạnh góc vuông a, b là bao nhiêu?- Diện tịch cả tấm bìa hình vuông cạnh a+ b bằng bao...
Đọc tiếp
Lấy giấy trắng cắt bốn tam giác vuông bằng nhau. Gọi a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền của các tam giác vuông này. Cắt một hình vuông bằng tấm bìa có cạnh dài a+b. Dán bốn tam giác vuông lên tấm bìa như Hình 9.32
- Dùng ê ke kiểm tra phần bìa không bị che lấp có phải là hình vuông cạnh bằng c không. Từ đó tính diện tích phần bìa này theo c
- Tổng diện tích bốn tam giác vuông có độ dài hai cạnh góc vuông a, b là bao nhiêu?
- Diện tịch cả tấm bìa hình vuông cạnh a+ b bằng bao nhiêu?
- So sánh \({c^2} + 2{\rm{a}}b\) với \({\left( {a + b} \right)^2}\)để rút ra nhận xét về mối quan hệ giữa hai đại lượng \({c^2}\) và \({a^2} + {b^2}\).
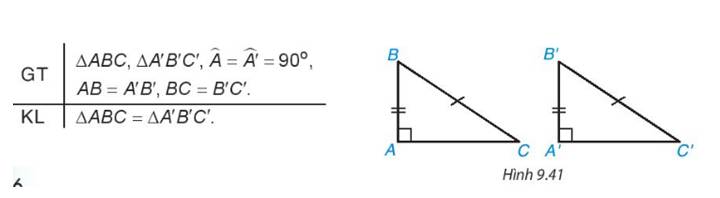
Trước đây chúng ta thừa nhận định lí về trường hợp bằng nhau đặc biệt của hai tam giác vuông: "Nếu một cạnh góc vuông và cạnh huyền của tam giác vuông này bằng một cạnh góc vuông và cạnh huyền của tam giác vuông kia thì hai tam giác vuông đó bằng nhau”.
Cho tam giác ABC cân tại đỉnh A, chiều cao AH=3cm và cạnh đáy BC=10cm. Hãy tính độ dài các cạnh bên AB, AC.
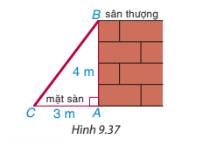
Trở lại tình huống mở đầu. xem thành cầu thang như cạnh huyền BC của tam giác vuông ABC (hình 9.37). Tù đó, hãy tính độ dài cạnh BC để suy ra chiều dài cầu thang cần xây.
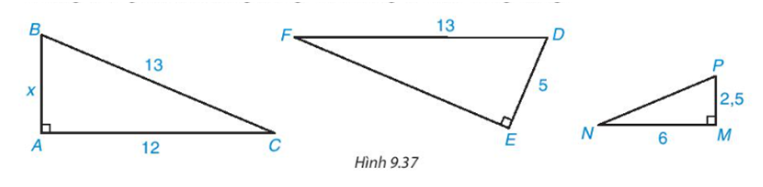
Cho tam giác vuông với kích thước như Hình 9.37. Hãy tính độ dài x và cho biết những tam giác nào đồng dạng, viết đúng kí hiệu đồng dạng
Cho tam giác ABC vuông tại A. Trong các khẳng định sau đây, khẳng định nào đúng, khẳng định nào sai:
a) \(A{B^2} + B{C^2} = A{C^2}\)
b) \(B{C^2} - A{C^2} = A{B^2}\)
c) \(A{C^2} + B{C^2} = A{B^2}\)
d) \(B{C^2} - A{B^2} = A{C^2}\)


