Người ta ném một hòn đá từ vách đá ở bờ biển xuống dưới. Hòn đá chạm vào mặt biển với vận tốc v có thành phần thẳng đứng xuống dưới là v1 và thành phần ngang là v2. Biết vận tốc v = 24 m/s, v1 = 17 m/s.
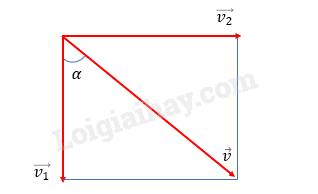
a) Vẽ sơ đồ các vectơ thể hiện các vận tốc.
b) Sử dụng sơ đồ để tìm v2.
c) Sử dụng sơ đồ để tìm góc giữa vận tốc của viên đá và phương thẳng đứng khi nó chạm vào mặt nước.
a)
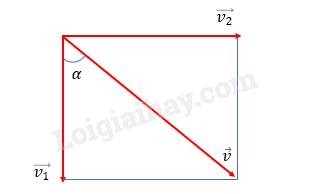
b) Ta có: v = 24 (m/s); v1 = 17 m/s
Từ sơ đồ, ta có: \({v^2} = v_1^2 + v_2^2\) (theo định lí Pytago trong 1 tam giác vuông)
=> \({v_2} = \sqrt {{v^2} - v_1^2} = \sqrt {{{24}^2} - {{17}^2}} \approx 16,94(m/s)\)
c) Gọi góc hợp bởi \(\overrightarrow v \) và \(\overrightarrow {{v_1}} \) là \(\alpha \)
Góc giữa vận tốc của viên đá và phương thẳng đứng khi nó chạm vào mặt nước là:
\(\cos \alpha = \frac{{{v_1}}}{v} = \frac{{17}}{{24}} \Rightarrow \alpha \approx {44^0}54'\)